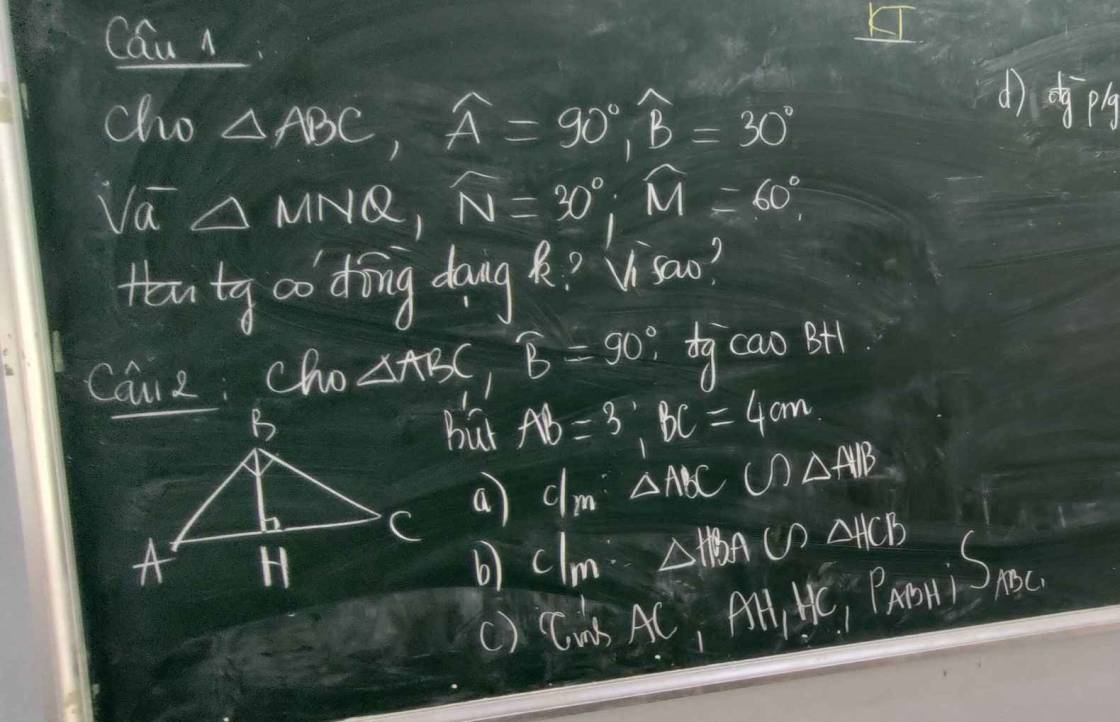Câu 1
xét ΔABC có
\(\widehat{A}\)+\(\widehat{B}\)+\(\widehat{C}\)=180\(^o\)
=>\(\widehat{C}\)=180\(^o\)-\(\widehat{A}\)-\(\widehat{B}\)
=180\(^o\)-90\(^o\)-30\(^o\)
=180\(^o\)-(90\(^o\)+30\(^o\))
=180\(^o\)-120\(^o\)
=60\(^o\)
Xét ΔABC và ΔMNQ ta có
\(\widehat{M}\)=\(\widehat{C}\)=60\(^o\)
\(\widehat{N}\)=\(\widehat{B}\)=30\(^o\)
=>ΔABC ∼ΔMNQ(g,g)
Câu 2
Xét ΔABC và ΔAHB ta có
\(\widehat{A}\) chung
\(\widehat{ABC}\)=\(\widehat{AHB}\)=90\(^o\)
=>ΔABC∼ΔAHB(1)
Xét ΔHCB và ΔABC ta có
\(\widehat{C}\) chung
\(\widehat{AHC}\)=\(\widehat{ABC}\)=90\(^o\)
=>ΔABC ∼ ΔAHC(2)
Từ (1)và(2)=>ΔHBA∼ΔHCB
c)áp dụng định lí pytago ta có
AB\(^2\)+BC\(^2\)=AC\(^2\)
=>AC=\(\sqrt{AB^2+BC^2}\)
=\(\sqrt{3^2+4^2}\)
=\(\sqrt{25}\)
=5
Vậy AC = 5cm