Question

Answer 1

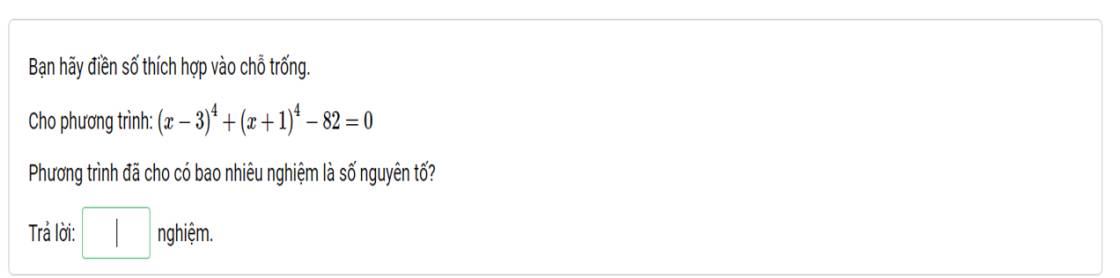
Lời giải:
Đặt $x-1=a$ thì pt trở thành:
$(a-2)^4+(a+2)^4-82=0$

$\Leftrightarrow 2a^4+48a^2-50=0$

$\Leftrightarrow a^4+24a^2-25=0$

$\Leftrightarrow (a^4-a^2)+(25a^2-25)=0$

$\Leftrightarrow a^2(a^2-1)+25(a^2-1)=0$
$\Leftrightarrow (a^2+25)(a^2-1)=0$

$\Leftrightarrow a^2-1=0$

$\Leftrightarrow a=\pm 1$

$\Leftrightarrow x-1=\pm 1$

$\Leftrightarrow x=0$ hoặc $x=2$

Vậy pt có 1 nghiệm $x=2$ là số nguyên tố.