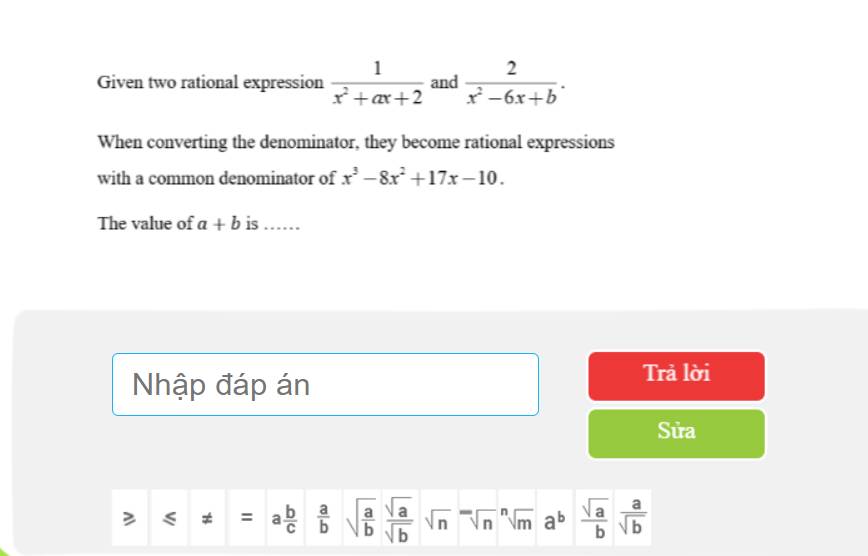
\(x^3-8x^2+17x-10\)
\(=x^3-x^2-7x^2+7x+10x-10\)
\(=x^2\left(x-1\right)-7x\left(x-1\right)+10\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2-7x+10\right)\)
\(=\left(x-1\right)\left(x^2-2x-5x+10\right)\)
\(=\left(x-1\right)\left[x\left(x-2\right)-5\left(x-2\right)\right]\)
\(=\left(x-1\right)\left(x-2\right)\left(x-5\right)\)
Mẫu chung của \(x^2+ax+2\left(1\right)\) và \(x^2-6x+b\left(2\right)\) là
\(x^3-8x^2+17x-10=\left(x-1\right)\left(x-2\right)\left(x-5\right)\)
Ta thấy \(\left(x-1\right)\left(x-2\right)=x^2-3x+2\) cùng chung hệ số tự do với đa thức (1) là 2.
\(\Rightarrow x^2+ax+2=x^2-3x+2\Rightarrow a=-3\)
Mặt khác \(\left(x-1\right)\left(x-5\right)=x^2-6x+5\) cùng chung hệ số bậc nhất với đa thức (2) là -6.
\(\Rightarrow x^2-6x+5=x^2-6x+b\Rightarrow b=5\)
The value of \(a+b\) is \(-3+5=2\) :)