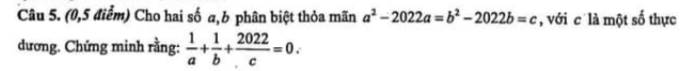\(a^2-2022a=b^2-2022b\)
\(\Rightarrow a^2-b^2-2022\left(a-b\right)=0\)
\(\Rightarrow\left(a-b\right)\left(a+b\right)-2022\left(a-b\right)=0\)
\(\Rightarrow\left(a-b\right)\left(a+b-2022\right)=0\)
Vì a,b là 2 số phân biệt nên \(a+b-2022=0\Rightarrow b=2022-a\).
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{2022}{c}=\dfrac{1}{a}+\dfrac{1}{2022-a}+\dfrac{2022}{a^2-2022a}\)
\(=\dfrac{1}{a}+\dfrac{1}{2022-a}-\dfrac{2022}{a\left(2022-a\right)}\)
\(=\dfrac{2022-a+a-2022}{a\left(2022-a\right)}=0\left(đpcm\right)\)
Đúng 0
Bình luận (0)
