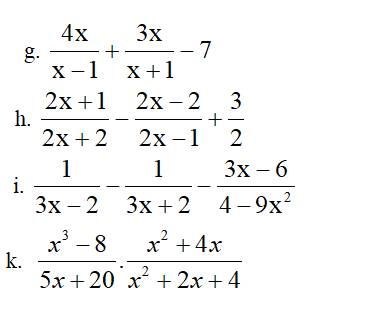Question

Answer 1

g: \(=\dfrac{4x^2+4x+3x^2-3x-7x^2+7}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+7}{\left(x-1\right)\left(x+1\right)}\)

h: \(=\dfrac{4x^2-1-4x^2+4}{\left(2x+2\right)\left(2x-1\right)}+\dfrac{3\left(x+1\right)\left(2x-1\right)}{2\left(x+1\right)\left(2x-1\right)}\)

\(=\dfrac{3+3\left(2x^2-x+2x-1\right)}{2\left(x+1\right)\left(2x-1\right)}\)

\(=\dfrac{3+6x^2+3x-3}{2\left(x+1\right)\left(2x-1\right)}=\dfrac{6x^2+3x}{2\left(x+1\right)\left(2x-1\right)}\)

i: \(=\dfrac{3x+2-3x+2+3x-6}{\left(3x-2\right)\left(3x+2\right)}=\dfrac{3x-2}{\left(3x-2\right)\left(3x+2\right)}=\dfrac{1}{3x+2}\)