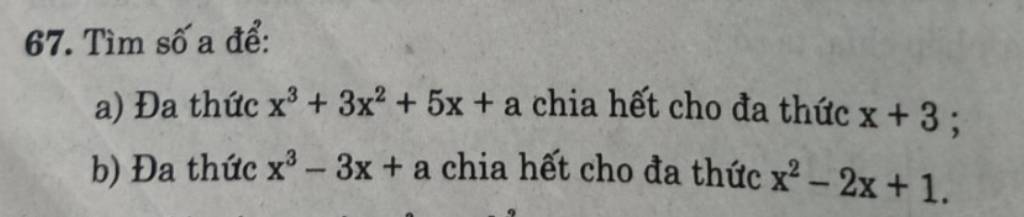Lời giải:
a. Đặt $f(x)=x^3+3x^2+5x+a$.
Theo định lý Bê-du, để $f(x)\vdots x+3$ thì:
$f(-3)=0$
$\Leftrightarrow (-3)^3+3(-3)^2+5(-3)+a=0$
$\Leftrightarrow a=15$
b.
$x^3-3x+a=x(x^2-2x+1)+2x^2-4x+a$
$=x(x^2-2x+1)+2(x^2-2x+1)+a-2$
$=(x+2)(x^2-2x+1)+a-2$
Vậy $x^3-3x+a$ chia $x^2-2x+1$ dư $a-2$. Để đây là phép chia hết thì $a-2=0$
$\Leftrightarrow a=2$
Wiao Đz : nếu bạn chưa học định lý Bê-du thì cũng đơn giản thôi.
Bạn biến đổi đa thức về dạng có chứa $x+3$ để tìm số dư, như cách làm phần b.
$x^3+3x^2+5x+a=x^2(x+3)+5(x+3)+(a-15)$
$=(x+3)(x^2+5)+(a-15)$
Vậy $x^3+3x^2+5x+a$ chia $x+3$ dư $a-15$
Để đây là phép chia hết thì $a-15=0\Leftrightarrow a=15$