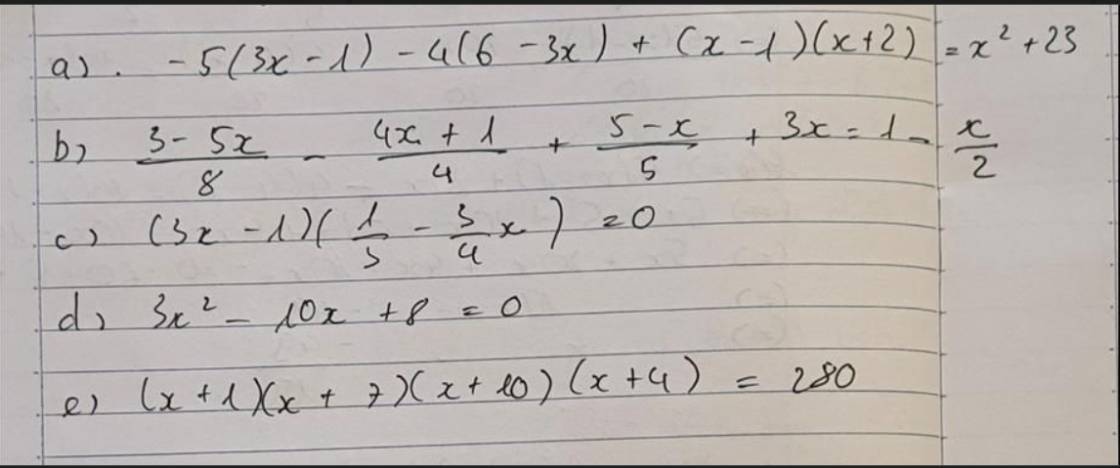`a.`\(-5\left(3x-1\right)-4\left(6-3x\right)+\left(x-1\right)\left(x+2\right)=x^2+23\)
\(\Leftrightarrow-15x+5-24+12x+x^2-x-2=x^2+23\)
\(\Leftrightarrow-4x=44\)
`<=>x=-11`
Vậy \(S=\left\{-11\right\}\)
`b.`\(\dfrac{3-5x}{8}-\dfrac{4x+1}{4}+\dfrac{5-x}{5}+3x=1-\dfrac{x}{2}\)
\(\Leftrightarrow\dfrac{5\left(3-5x\right)-10\left(4x+1\right)+8\left(5-x\right)+120x}{40}=\dfrac{40-20x}{40}\)
\(\Leftrightarrow5\left(3-5x\right)-10\left(4x+1\right)+8\left(5-x\right)+120x=40-20x\)
\(\Leftrightarrow15-25x-40x-10+40-8x+120x=40-20x\)
\(\Leftrightarrow67x=-5\)
`<=>x=-5/67`
Vậy \(S=\left\{-\dfrac{5}{67}\right\}\)
`c.`\(\left(3x-1\right)\left(\dfrac{1}{3}-\dfrac{3}{4}x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=0\\\dfrac{1}{3}-\dfrac{3}{4}x=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=\dfrac{4}{9}\end{matrix}\right.\)
Vậy \(S=\left\{\dfrac{1}{3};\dfrac{4}{9}\right\}\)
`d.`\(3x^2-10x+8=0\)
\(\Leftrightarrow\left(x-2\right)\left(3x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\3x-4=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{4}{3}\end{matrix}\right.\)
Vậy \(S=\left\{2;\dfrac{4}{3}\right\}\)
`e.`\(\left(x+1\right)\left(x+7\right)\left(x+10\right)\left(x+4\right)=280\)
\(\Leftrightarrow\left(x+1\right)\left(x+10\right)\left(x+7\right)\left(x+4\right)=280\)
\(\Leftrightarrow\left(x^2+11x+10\right)\left(x^2+11x+28\right)=280\)
Đặt \(x^2+11x+10=t\)
\(\Leftrightarrow t\left(t+18\right)=280\)
\(\Leftrightarrow t^2+18t-280=0\)
\(\Leftrightarrow\left(t-10\right)\left(t+28\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=10\\t=-28\end{matrix}\right.\)
`@` Với \(t=10\) \(\Rightarrow x^2+11x+10=10\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-11\end{matrix}\right.\)
`@`Với \(t=-28\) \(\Rightarrow x^2+11x+10=-28\)
\(\Leftrightarrow x^2+11x+38=0\) ( vô nghiệm )
Vậy \(S=\left\{0;-11\right\}\)