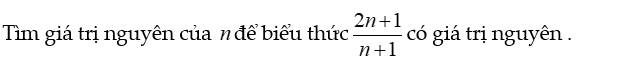Question

Answer 1

   `n \ne -1,n in ZZ`

`[2n+1]/[n+1]=[2n+2-1]/[n+1]=[2(n+1)-1]/[n+1]=2-1/[n+1]`

Để `[2n+1]/[n+1]` có giá trị nguyên thì `2-1/[n+1] in ZZ`

   Hay `1/[n+1] in ZZ`

  `=>n+1 in Ư_1`

Mà `Ư_1={+-1}`

`@n+1=1=>n=0` (t/m)

`@n+1=-1=>n=-2` (t/m)

Vậy `n in {0;-2}`

Answer 2

\(\dfrac{2n+1}{n+1}=2-\dfrac{1}{n+1}\)

\(n+1\inƯ\left(1\right)\) 

mà \(Ư\left(1\right)=\left\{1;-1\right\}\)

Vậy ....

\(\left\{{}\begin{matrix}n+1=1\\n+1=-1\end{matrix}\right.=>\left\{{}\begin{matrix}n=0\\n=-2\end{matrix}\right.\)