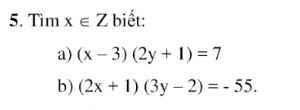a, \(\left(x-3\right)\left(2y+1\right)=7\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-3=1\\2y+1=7\end{matrix}\right.\\\left\{{}\begin{matrix}x-3=7\\2y+1=1\end{matrix}\right.\\\left\{{}\begin{matrix}x-3=-1\\2y+1=-7\end{matrix}\right.\\\left\{{}\begin{matrix}x-3=-7\\2y+1=-1\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=4\\y=3\end{matrix}\right.\\\left\{{}\begin{matrix}x=10\\y=0\end{matrix}\right.\\\left\{{}\begin{matrix}x=2\\y=-4\end{matrix}\right.\\\left\{{}\begin{matrix}x=-4\\y=-1\end{matrix}\right.\end{matrix}\right.\)
Vậy \(\left(x;y\right)\in\left\{\left(4;3\right),\left(10;0\right),\left(2;-4\right),\left(-4;-1\right)\right\}\)
b, \(\Rightarrow2x+1;3y-2\inƯ\left(-55\right)=\left\{\pm1;\pm55\right\}\)
| 2x+1 | 1 | -1 | 55 | -55 |
| 3y-2 | -55 | 55 | -1 | 1 |
| x | 0 | -1 | 27 | -28 |
| y | loại | loại | loại | 1 |
`a)(x-3)(2y+1)=7`
`=>(x-3)(2y+1)=7.1=(-7).(-1)`
`@TH1:{(x-3=7=>x=10),(2y+1=1=>y=0):}`
`@TH2:{(x-3=1=>x=4),(2y+1=7=>y=3):}`
`@TH3:{(x-3=-1=>x=2),(2y+1=-7=>y=-4):}`
`@TH4:{(x-3=-7=>x=-4),(2y+1=-1=>y=-1):}`
___________________________________________
`b)(2x+1)(3y-2)=-55`
`=>(2x+1)(3y-2)=-5.11=-11.5=-55.1=-1.55`
`@TH1:{(2x+1=-5=>x=-3),(3y-2=11=>y=13/3):}` (Loại)
`@TH2:{(2x+1=11=>x=5),(3y-2=-5=>y=-1):}`
`@TH3:{(2x+1=-11=>x=-6),(3y-2=5=>y=7/3):}` (Loại)
`@TH4:{(2x+1=5=>x=2),(3y-2=-11=>y=-3):}`
`@TH5:{(2x+1=-55=>x=-28),(3y-2=1=>y=1):}`
`@TH6:{(2x+1=1=>x=0),(3y-2=-55=>y=-53/3):}` (Loại)
`@TH7:{(2x+1=-1=>x=-1),(3y-2=55=>y=19):}`
`@TH8:{(2x+1=55=>x=27),(3y-2=-1=>y=1/3):}` (Loại)