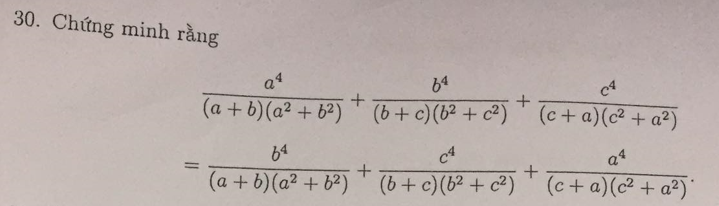Ta có \(\dfrac{a^4}{\left(a+b\right)\left(a^2+b^2\right)}-\dfrac{b^4}{\left(a+b\right)\left(a^2+b^2\right)}=\dfrac{\left(a-b\right)\left(a+b\right)\left(a^2+b^2\right)}{\left(a+b\right)\left(a^2+b^2\right)}=a-b\)Chứng minh tương tự, ta có
\(\dfrac{b^4}{\left(b+c\right)\left(b^2+c^2\right)}-\dfrac{c^4}{\left(b+c\right)\left(b^2+c^2\right)}=b-c\)
\(\dfrac{c^4}{\left(c+a\right)\left(c^2+a^2\right)}-\dfrac{a^4}{\left(c+a\right)\left(c^2+a^2\right)}=c-a\)
=> Hiệu của 2 vế là a - b + b - c + c - a = 0
=> 2 vế bằng nhau (đpcm)
Đúng 1
Bình luận (0)
