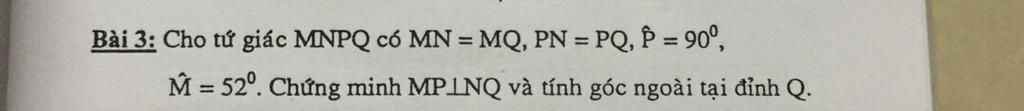Question

Answer 1

\(MN=MQ\Rightarrow\)M nằm trên đường trung trực của đoạn NQ (1)

\(PN=PQ\Rightarrow\)P nằm trên đường trung trực của đoạn NQ (2)

Từ (1), (2) suy ra:

MP là đường trung trực của NQ.

\(\Rightarrow\)MP⊥NQ.

△MNQ cân tại M \(\Rightarrow\widehat{MQN}=\dfrac{180^0-\widehat{NMQ}}{2}=\dfrac{180^0-52^0}{2}=64^0\)

△NPQ cân tại P \(\Rightarrow\widehat{NQP}=\dfrac{180^0-\widehat{NPQ}}{2}=\dfrac{180^0-90^0}{2}=45^0\)

\(\widehat{MQP}=\widehat{MQN}+\widehat{NQP}=64^0+45^0=109^0\)

\(\Rightarrow\widehat{MQP}'=180^0-\widehat{MQP}=180^0-109^0=71^0\)