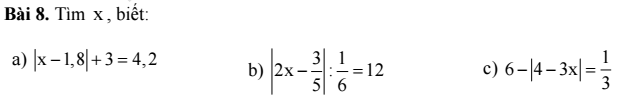`a)|x-1,8|+3=4,2`
`<=>|x-1,8|=1,2`
`<=>` $\left[\begin{matrix} x-1,8=1,2\\ x-1,8=-1,2\end{matrix}\right.$
`<=>` $\left[\begin{matrix} x=3\\ x=0,6\end{matrix}\right.$
__________________________________________________________
`b)|2x-3/5|:1/6=12`
`<=>|2x-3/5|=2`
`<=>` $\left[\begin{matrix} 2x-\dfrac{3}{5}=2\\ 2x-\dfrac{3}{5}=-2\end{matrix}\right.$
`<=>` $\left[\begin{matrix} x=\dfrac{13}{10}\\ x=\dfrac{-7}{10}\end{matrix}\right.$
__________________________________________________________
`c) 6-|4-3x|=1/3`
`<=>|4-3x|=17/3`
`<=>` $\left[\begin{matrix} 4-3x=\dfrac{17}{3}\\ 4-3x=\dfrac{-17}{3}\end{matrix}\right.$
`<=>` $\left[\begin{matrix} x=\dfrac{-5}{9}\\ x=\dfrac{29}{9}\end{matrix}\right.$
a) \(\left|x-1,8\right|+3=4,2\\ \Leftrightarrow\left|x-1,8\right|=1,2\\ \Leftrightarrow\left[{}\begin{matrix}x-1,8=1,2\\x-1,8=-1,2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=0,6\end{matrix}\right.\)
Vậy \(x\in\left\{3;0,6\right\}\)
b) \(\left|2x-\dfrac{3}{5}\right|:\dfrac{1}{6}=12\\ \Leftrightarrow\left|2x-\dfrac{3}{5}\right|=12\cdot\dfrac{1}{6}\\ \Leftrightarrow\left|2x-\dfrac{3}{5}\right|=2\\ \Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{3}{5}=2\\2x-\dfrac{3}{5}=-2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{13}{5}\\2x=\dfrac{-7}{5}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{13}{10}\\x=\dfrac{-7}{10}\end{matrix}\right.\)
Vậy \(x\in\left\{\dfrac{13}{10};\dfrac{-7}{10}\right\}\)
c) \(6-\left|4-3x\right|=\dfrac{1}{3}\\ \Leftrightarrow\left|4-3x\right|=6-\dfrac{1}{3}\\ \Leftrightarrow\left|4-3x\right|=\dfrac{17}{3}\\ \Leftrightarrow\left[{}\begin{matrix}4-3x=\dfrac{17}{3}\\4-3x=\dfrac{-17}{3}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}3x=4-\dfrac{17}{3}=\dfrac{-5}{3}\\3x=4+\dfrac{17}{3}=\dfrac{29}{3}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-5}{6}\\x=\dfrac{29}{6}\end{matrix}\right.\)
Vậy \(x\in\left\{\dfrac{-5}{6};\dfrac{29}{6}\right\}\)