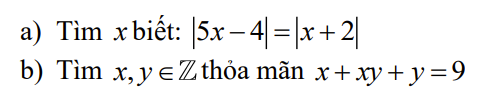Question

Answer 1

`a)`

`|5x-4| = |x+2|`

`<=> 5x - 4 = x+2` hoặc `5x - 4 = -( x+2)`

`<=> 4x = 6` hoặc `5x - 4 = -x - 2`

`<=> x = 3/2` hoặc `x = 1/3`

Vậy `S={3/2 ; 1/3}`

 

Answer 2

`a)`

Ta có dạng tổng quát `: |f(x)| = |g(x)|`

`-> f(x) = g(x)` hoặc `f(x) = -g(x)` 

Answer 3

`b)`

`x + xy + y = 9`

`<=> x( y + 1 ) + ( y + 1 ) = 10`

`<=> ( x + 1 )( y + 1 ) = 10`

Do `x;y in ZZ`

`-> x + 1 ; y + 1 in Ư_{(10)} = { +-1 ; +-2 ; +-5 ; +-10 }`

Th1 `:`

`{(x+1=1),(y+1=10):}`

`<=>` `{(x=0),(y=9):}`

Th2 `:`

`{(x+1=2),(y+1=5):}`

`<=>` `{(x=1),(y=4):}`

Th3 `:`

`{(x+1=5),(y+1=2):}`

`<=>` `{(x=4),(y=1):}`

Th4 `:`

`{(x+1=10),(y+1=11):}`

`<=>` `{(x=9),(y=0):}`

Th5 `;`

`{(x+1=-1),(y+1=-10):}`

`<=>` `{(x=-2),(y=-11):}`

Th6 `:`

`{(x+1=-2),(y+1=-5):}`

`<=>` `{(x=-3),(y=-6):}`

Th7 `;`

`{(x+1=-5),(y+1=-2):}`

`<=>` `{(x=-6),(y=-3):}`

Th8 `:`

`{(x+1=-10),(y+1=-1):}`

`<=>` `{(x=-11),(y=-2):}`

Vậy `....`