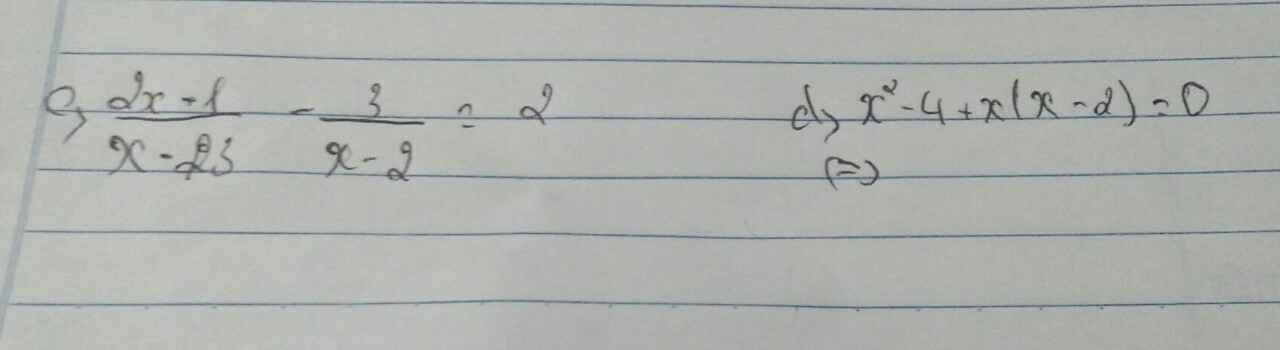`a)[2x-1]/[x-3]-3/[x-2]=2` `ĐK: x \ne 2,x \ne 3`
`<=>[(2x-1)(x-2)-3(x-3)]/[(x-2)(x-3)]=[2(x-2)(x-3)]/[(x-2)(x-3)]`
`=>2x^2-4x-x+2-3x+9=2x^2-6x-4x+12`
`<=>2x=1`
`<=>x=1/2` (t/m)
Vậy `S={1/2}`
___________________________________________________
`d)x^2-4+x(x-2)=0`
`<=>x^2-4+x^2-2x=0`
`<=>2x^2-2x-4=0`
`<=>x^2-x-2=0`
`<=>x^2-2x+x-2=0`
`<=>(x-2)(x+1)=0`
`<=>x=2` hoặc `x=-1`
Vậy `S={-1;2}`
a) \(\dfrac{2x-1}{x-3}-\dfrac{3}{x-2}=2\) ĐK: x\(\ne3;x\ne2\)
<=>\(\dfrac{\left(2x-1\right).\left(x-2\right)}{\left(x-3\right).\left(x-2\right)}-\dfrac{3.\left(x-3\right)}{\left(x-3\right).\left(x-2\right)}-\dfrac{2.\left(x-2\right).\left(x-3\right)}{\left(x-2\right).\left(x-3\right)}=0\)
=>\(\left(2x-1\right).\left(x-2\right)-3x+9-\left(2x-4\right).\left(x-3\right)=0\)
<=>\(2x^2-x-4x+2-3x+9-\left(2x^2-4x-6x+12\right)=0\)
<=>\(2x^2-8x+11-2x^2+4x+6x-12=0\)
<=>\(2x=1\)
<=>\(x=\dfrac{1}{2}\) (TMĐK)
Vậy phương trình có tập nghiệm S=\(\left\{\dfrac{1}{2}\right\}\)
b) \(x^2-4+x.\left(x-2\right)=0\)
<=>\(\left(x-2\right).\left(x+2\right)+x.\left(x-2\right)=0\)
<=>\(\left(x-2\right).\left(x+2+x\right)=0\)
<=>\(\left(x-2\right).\left(2x+2\right)=0\)
<=>\(\left(x-2\right).2.\left(x+1\right)=0\)
<=>\(\left(x-2\right).\left(x+1\right)=0\) (vì 2>0)
<=>\(\left[{}\begin{matrix}\left(x-2\right)=0\\\left(x+1\right)=0\end{matrix}\right.\)
<=>\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Vậy phương trình có tập nghiệm S=\(\left\{2;-1\right\}\)