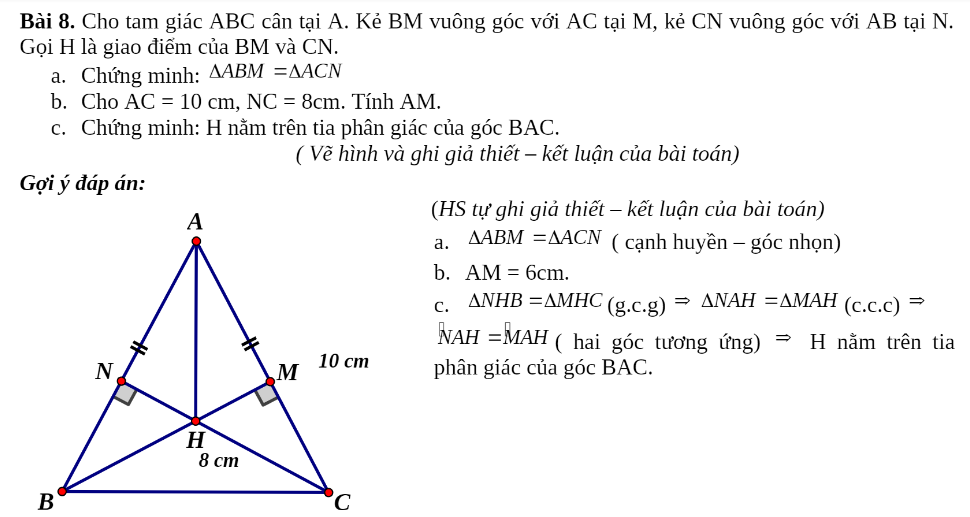
a,
Xét \(\triangle ABM\) vuông tại \(M\) và \(\triangle ACN\) vuông tại \(N \) ta có :
\(AB=AC\) ( \(\triangle ABC\) cân tại \(A\) )
Chung \(\widehat{A}\)
\(\Rightarrow\) \(\triangle ABM=\) \(\triangle ACN\) ( ch-gn )
\(\Rightarrow\) \(\begin{cases} BM=CN\\AN=AM \end{cases}\) ( các cặp cạnh tương ứng )
b,
Do \(\triangle ACN\) vuông tại \(N\)
\(\Rightarrow AN^2 + NC^2 = AC^2\) ( theo định lý Py-ta-go )
\(\Rightarrow\) \(AN = \sqrt{AC^2 - NC^2} = \sqrt{AB^2-BM^2} = \sqrt{10^2 - 8^2} =6 = AM\)
Vậy \(AM=6\) cm .
c,
Do \(\triangle ABC\) cân tại A .
=> \(\widehat{B}=\widehat{C}\) (1)
Do \(\triangle ABM=\triangle ACN\)
=> \(\widehat{ABH} = \widehat{ACH}\) (2)
Từ (1) và (2)
=> \(\widehat{HBC}=\widehat{HCB}\)
=> \(\triangle HBC\) cân tại A \(\Leftrightarrow HB=HC\)
Xét \(\triangle ABH\) và \(\triangle ACH\) ta có :
\(AB=AC\)
\(AH\) chung
\(HB=HC\)
=> \(\triangle ABH = \triangle ACH\) ( c.c.c )
=> \(\widehat{BAH}=\widehat{CAH}\)
=> \(AH\) là tia phân giác \(\widehat{BAC}\) hay \(H \in\) tia phân giác \(\widehat{BAC}\)