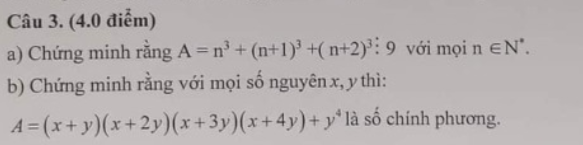b) A=(x+y)(x+2y)(x+3y)(x+4y)+y^4
\(A=[(x+y)(x+4y)][(x+2y)(x+4y)]+y^4 \)
\(A=(x^2+5xy+4y^2)(x^2+6xy+8y^2)+ y^4\)
\(A=x^4+35x^3y+42x^2y^2+40xy^3+33y^4\)
Táh ra ta được
A là mọt số chính phương
b)\(A=\left(x+y\right)\left(x+2y\right)\left(x+3y\right)\left(x+4y\right)+y^4\)
\(=\left(x+y\right)\left(x+4y\right)\left(x+2y\right)\left(x+3y\right)+y^4\)
\(=\left(x^2+4xy+xy+4y^2\right)\left(x^2+3xy+2xy+6y^2\right)+y^4\)
\(=\left(x^2+5xy+4y^2\right)\left(x^2+5xy+6y^2\right)+y^4\)
\(=\left(x^2+5xy+4y^2\right)\left(x^2+5xy+4y^2+2y^2\right)+y^4\)
\(=\left(x^2+5xy+4y^2\right)^2+2\left(x^2+5xy+4y^2\right)y^2+y^4\)
\(=\left(x^2+5xy+4y^2+y^2\right)^2=\left(x^2+5xy+5y^2\right)^2\)
a) \(\left(a+b+c\right)^3=a^3+3a^2\left(b+c\right)+3a\left(b+c\right)^2+\left(b+c\right)^3\)
\(=a^3+3a\left(b+c\right)\left(a+b+c\right)+b^3+c^3+3b^2c+3bc^2\)
\(=a^3+3a\left(b+c\right)\left(a+b+c\right)+b^3+c^3+3bc\left(b+c\right)\)
\(=a^3+b^3+c^3+3\left(b+c\right)\left(a^2+ab+ac+bc\right)\)
\(=a^3+b^3+c^3+3\left(b+c\right)\left[a\left(a+b\right)+c\left(a+b\right)\right]\)
\(=a^3+b^3+c^3+3\left(b+c\right)\left(a+b\right)\left(a+c\right)\)
\(\Rightarrow a^3+b^3+c^3=\left(a+b+c\right)^3-3\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
\(A=n^3+\left(n+1\right)^3+\left(n+2\right)^3=\left(n+n+1+n+2\right)^3-3\left(n+n+1\right)\left(n+1+n+2\right)\left(n+2+n\right)\)\(=\left(3n+3\right)^3-3\left(2n+1\right)\left(2n+3\right)\left(2n+1\right)\)
\(=27\left(n+1\right)^3-3\left(2n+1\right)\left(2n+3\right)\left(2n+2\right)\)
-Ta c/m \(\left(2n+1\right)\left(2n+3\right)\left(2n+2\right)⋮3\) (*)
*\(2n+1=3k\Rightarrow\) (*)⋮3
*\(2n+1=3k+1\Rightarrow2n+3=3k+3\) (*)⋮3
*\(2n+1=3k+2\Rightarrow2n+2=3k+3\) (*)⋮3
\(\Rightarrow\)(*)⋮3
\(\Rightarrow3\left(2n+1\right)\left(2n+2\right)\left(2n+3\right)⋮9\)
Mà \(27\left(n+1\right)^3⋮9\Rightarrow A⋮9\)