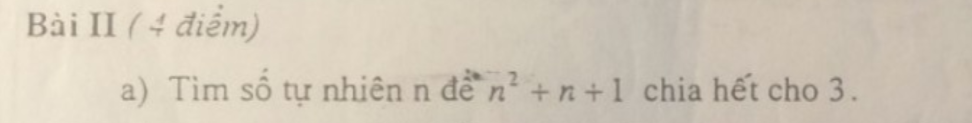-Xét \(n=3k\):
\(n^2+n+1=9k^2+3k+1\) chia 3 dư 1 (loại)
-Xét \(n=3k+1\):
\(n^2+n+1=\left(3k+1\right)^2+3k+1+1=9k^2+6k+1+3k+1+1=9k^2+9k+3\)
chia hết cho 3 (nhận)
-Xét \(n=3k+2\):
\(n^2+n+1=\left(3k+2\right)^2+3k+2+1=9k^2+12k+4+3k+2+1=9k^2+21k+7\)
chia 3 dư 1 (loại)
-Vậy \(n=3k+1\) (n chia 3 dư 1) thì \(n^2+n+1\) chia hết cho 3.
GIẢI PHƯƠNG TRÌNH
1)\(\dfrac{x+1}{35}+\dfrac{x+3}{33}=\dfrac{x+5}{31}+\dfrac{x+7}{29}\)
2)x(x+1)(x+2)(x+3)=24
3)\(\dfrac{x-1}{13}-\dfrac{2x-13}{15}=\dfrac{3x-15}{27}-\dfrac{4x-27}{29}\)
4)\(\dfrac{1909-x}{91}+\dfrac{1907-x}{93}+\dfrac{1905-x}{95}+\dfrac{1903-x}{91}+4=0\)
cho tam giác ABC biết AB=5cm , AC=10cm , BC=12cm .Trên AB và AC lần lượt lấy E và F sao cho AE=2cm ,AF=4cm
a, Tính EF ?
b,Tính tỉ số chu vi và diện tích của tam giác AEF và tam giác ABC
c, BF và CE cắt nhau tại I . CMR: IE.IB=IF.IC
x3 _ x2 _ 4x - 4 = 0
Ai giúp mình làm câu này đi ạ:(((( Mình cảm ơnn 🥺👉👈
Tìm giá trị trị nhỏ nhất của \(P=4a^2+4ab+4b^2-12a-12b+12\)
cho tam giác ABC nhọn,các đường cao AD,BE,CF cắt nhau tại Ha.Chứng minh:tam giác AEB đồng dạng tam giác AFCb.Chứng minh:tam giác AEF đồng dạng tam giác ABCc.cho thêm điều kiện 4AD.HD=BC.CHứng minh tam giác ABC cân
Mọi người giải giúp mình với ạ, mai mình kiểm tra rồi, mình cảm ơn
cho a,b,c là các số nguyên . Chứng minh rằng nếu a^2016 + b^2017 + c^2018 chia hết cho 6 thì a^2018 + b^2019 + c^2020 cũng chia hết cho 6.
Giúp mk với! :)
Giúp mk gấp câu 23 nha.
Cho hình chữ nhật ABCD . Gọi H là chân đường vuông góc kẻ từ A xuống BD.
a) Chứng minh: Tam giác AHB đồng dạng tam giác DAB.
b) Kẻ phân giác của
BCD
cắt BD ở E. Tính AH và diện tích tam giác AEH cho biết AB = 8cm,
BC = 6cm
mik cần ngay bh ạ!!
Cho biểu thức A=\(\frac{x^2+2x+3}{x^2+2}\).
a) Tìm GTNN, GTLN của A
b) Tìm x để A là số nguyên
