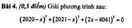-Đặt \(t=2020-x\)
\(\left(2020-x\right)^3+\left(2021-x\right)^3+\left(2x-4041\right)^3=0\)
\(\Leftrightarrow t^3+\left(t+1\right)^3+\left(-2t-1\right)^3=0\)
\(\Leftrightarrow\left(2t+1\right)\left[t^2-t\left(t+1\right)+\left(t+1\right)^2\right]-\left(2t+1\right)^3=0\)
\(\Leftrightarrow\left(2t+1\right)\left[t^2-t\left(t+1\right)+\left(t+1\right)^2-\left(2t+1\right)^2\right]=0\)
\(\Leftrightarrow\left(2t+1\right)\left[t^2-t^2-t+t^2+2t+1-4t^2-4t-1\right]=0\)
\(\Leftrightarrow\left(2t+1\right)\left[-3t^2-3t\right]=0\)
\(\Leftrightarrow-3t\left(2t+1\right)\left(t+1\right)=0\)
\(\Leftrightarrow t\left(2t+1\right)\left(t+1\right)=0\)
\(\Leftrightarrow t=0\) hay \(2t+1=0\) hay \(t+1=0\)
\(\Leftrightarrow2020-x=0\) hay \(2\left(2020-x\right)+1=0\) hay \(2020-x+1=0\)
\(\Leftrightarrow x=2020\) hay \(x=\dfrac{4041}{2}\) hay \(x=2021\)
-Vậy \(S=\left\{2020;\dfrac{4041}{2};2021\right\}\)
\(\Rightarrow2020-x+2021-x+2x-4041=0\)
\(\Leftrightarrow0x=0\)-> vậy pt có vô số nghiệm