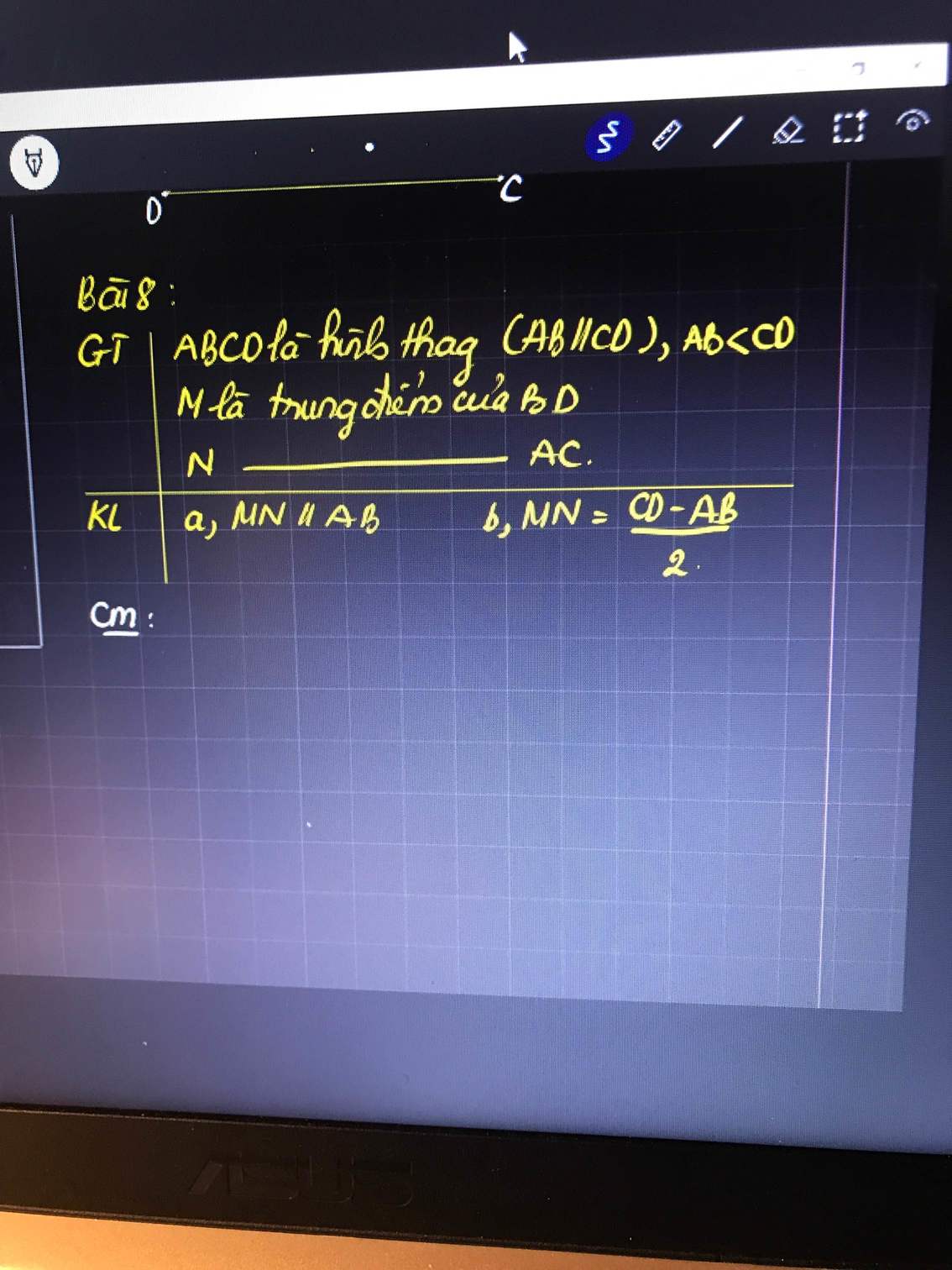
*AC và BD cắt nhau tại O.
-Xét △OAB có: AB//CD (gt)
\(\Rightarrow\dfrac{AO}{OC}=\dfrac{BO}{OD};\dfrac{AC}{OC}=\dfrac{BD}{OD}\) (định lí Ta-let)
Mà \(AC=2AN;BD=2BN\) (N là trung điểm AC, M là trung điểm BD).
\(\Rightarrow\dfrac{2AN}{OC}=\dfrac{2BM}{OD}\Rightarrow\dfrac{AN}{OC}=\dfrac{BM}{OC}\)
\(\Rightarrow\dfrac{AN}{OC}-\dfrac{AO}{OC}=\dfrac{BM}{OD}-\dfrac{BO}{OD}\)
\(\Rightarrow\dfrac{ON}{OC}=\dfrac{OM}{OD}\)
-Xét △OMN và △ODC có: \(\dfrac{ON}{OC}=\dfrac{OM}{OD}\) (cmt)
\(\Rightarrow\)MN//CD (định lí Ta-let đảo).
\(\Rightarrow\dfrac{DC}{MN}=\dfrac{OD}{OM}\) (định lí Ta-let)
\(\Rightarrow\dfrac{DC}{MN}-1=\dfrac{OD}{OM}-1\)
\(\Rightarrow\dfrac{DC-MN}{MN}=\dfrac{MD}{OM}\)
Mà \(MD=BM\) (M là trung điểm BD)
\(\Rightarrow\dfrac{DC-MN}{MN}=\dfrac{BM}{OM}\)
\(\Rightarrow\dfrac{DC-MN}{MN}-1=\dfrac{BM}{OM}-1\)
\(\Rightarrow\dfrac{DC-2MN}{MN}=\dfrac{OB}{OM}\)
-Xét △OAB có: MN//AB//CD.
\(\Rightarrow\dfrac{OB}{OM}=\dfrac{AB}{MN}\) (hệ quả định lí Ta-let)
Mà \(\dfrac{DC-2MN}{MN}=\dfrac{OB}{OM}\) (cmt)
\(\Rightarrow\dfrac{DC-2MN}{MN}=\dfrac{AB}{MN}\)
\(\Rightarrow DC-2MN=AB\)
\(\Rightarrow MN=\dfrac{DC-AB}{2}\)