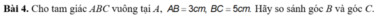Question

Answer 1

Xét tam giác vuông ABC có:

\(AB^2+AC^2=BC^2\)

\(=>3^2+AC^2=5^2\)

\(=>AC^2=25-9=16 \)

\(=>AC=4\)cm

=>AB<AC

=>C<B

Answer 2

Áp dụng định lý Pitago, ta có:
\(AC^2=BC^2-AB^2=5^2-3^2=16\left(cm\right)\Rightarrow AC=4\left(cm\right)\)

Dựa vào quan hệ giữa góc và cạnh trong tam giác:
\(AC>AB\Rightarrow\widehat{B}>\widehat{C}\)

 

Answer 3

\(\Delta ABC\) vuông tại A

Theo định lí Pytago -> \(AC^2=BC^2-AB^2\)  -> \(AC=4\left(cm\right)\)

Có : AB < AC

->  \(\widehat{ABC}>\widehat{ACB}\)