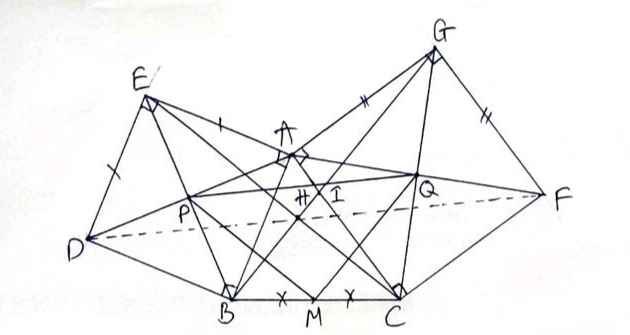
a, Xét Δ BCG có M và Q lần lượt là trung điểm của BC và CG
=> MQ là đường tb tam giác BCG (1)
tương tự vs tam giác BCE
có MP là đường tb (2)
Xét tam giác ABG và AEC có :
AE=AB
góc EAC = góc BAG ( = 90 độ + BAC)
AC=AG
<=> 2 tam giác ABG và AEC = nhau ( c-g-c) (3)
=> EC=BG
từ(1) và (2) ở trên tiếp tục suy ra:
\(\dfrac{1}{2}EC=\dfrac{1}{2}BG\Leftrightarrow MP=MQ\) (8)
gọi I là giao điểm của AC và HG
Xét 2 tam giác : AIG và HIC có:
góc AIG = góc HIC ( 2 góc đối đỉnh)
góc AGI = góc HCI ( do (3))
<=> tam giác AIG ∼ tam giác HIC (g-g)(4)
từ (4) suy ra : góc IHC = góc IAG =90 độ (5)
từ (5) suy ra : \(BG\perp EC\)
Mà : \(\left\{{}\begin{matrix}MP//EC\\MQ//BG\end{matrix}\right.\) nên \(MP\perp MQ\) (6)
từ (6) suy ra góc PMQ = 90 độ (7)
từ (8) và (7) suy ra tam giác PMQ vuông cân ( tại M) ( đpcm)
b/ Xét tứ giác EAHB có góc EAB = góc EAH = 90 độ
<=> tứ giác EAHB nội tiếp ( t/giác nt lớp 9 ms học mà)
mà tứ giác EADB nt ( hình vuông)
nên EAHD nội tiếp => góc EHD = góc EAD= 45 độ(9)
c/m tương tự ta có : góc GHF= góc GAF = 45 độ(10)
từ (9) và (10) suy ra:
góc DHE + góc DHG+ góc GHF = 45 độ +90 độ + 45 độ = 180 độ
=> D; H ; F thẳng hàng ( đpcm)
( có j ko hỉu thì hỏi!!)