a) Xét tam giác ABM có:
MD là p/g của góc AMB (gt)
=>\(\dfrac{BM}{AM}=\dfrac{DB}{DA}=\dfrac{3}{4}=0,75\)
b) Xét tam giác AMC có:
ME là phân giác của góc AMC (gt)
=>\(\dfrac{MC}{AM}=\dfrac{CE}{AE}=\dfrac{BM}{AM}\)
=>\(\dfrac{CE}{AE}=\dfrac{DB}{DA}\)
Xét tam giác ABC có:
\(\dfrac{CE}{AE}=\dfrac{DB}{DA}\)(cmt)
=>DE//BC (định lí Ta-let đảo)
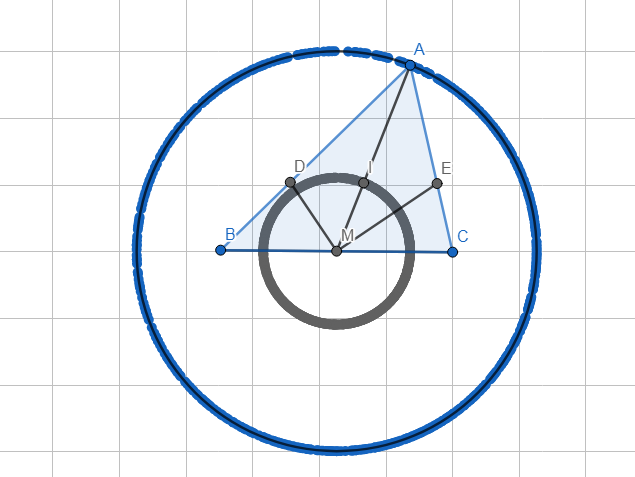
Khi BC cố định, AM=m thì A nằm trên đường tròn tâm M bán kính m (mình không biết kí hiệu nên ghi vậy).
* Tính MI theo a,m:
Xét tam giác ABM có:
DI//BM (cmt)
=>\(\dfrac{AD}{DB}=\dfrac{AI}{IM}=\dfrac{AM}{BM}\)
=>\(\dfrac{AM}{IM}=\dfrac{AM+BM}{BM}\)
=>\(\dfrac{m}{IM}=\dfrac{m+\dfrac{1}{2}a}{\dfrac{1}{2}a}\)
=>IM=\(\dfrac{\dfrac{1}{2}a.m}{\dfrac{1}{2}a +m}\)
Vậy tập hợp các giao điểm I của AM và DE là đường tròn tâm M bán kính
\(\dfrac{\dfrac{1}{2}a.m}{\dfrac{1}{2}a +m}\)