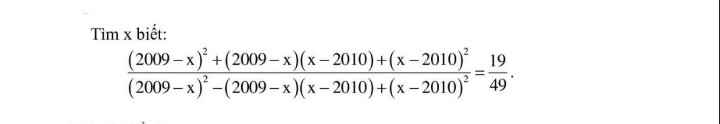Đặt \(\left\{{}\begin{matrix}2009-x=a\\x-2010=b\end{matrix}\right.\)
Phương trình trở thành:
\(\dfrac{a^2+ab+b^2}{a^2-ab+b^2}=\dfrac{19}{49}\)
\(\Rightarrow49a^2+49ab+49b^2=19a^2-19ab+19b^2\)
\(\Rightarrow30a^2-68ab+30b^2=0\)
\(\Rightarrow2\left(3a-5b\right)\left(5a-3b\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}3a=5b\\5a=3b\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}3\left(2009-x\right)=5\left(x-2010\right)\\5\left(2009-x\right)=3\left(x-2010\right)\end{matrix}\right.\)
\(\Rightarrow...\)
Đúng 0
Bình luận (0)
