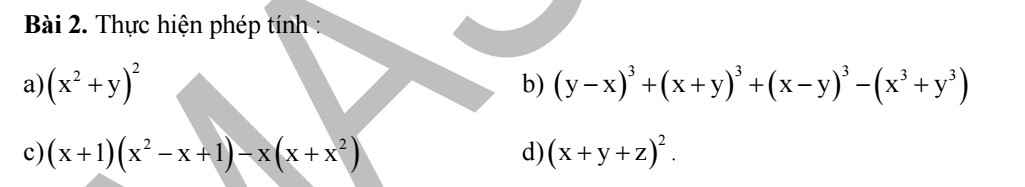\(a,=x^4+2x^2y+y^2\\ b,=\left[\left(y-x\right)^3+\left(x-y\right)^3\right]+\left[\left(x+y\right)^3-x^3-y^3\right]\\ =\left[-\left(x-y\right)^3+\left(x-y\right)^3\right]+\left(x^3+3x^2y+3xy^2+y^3-x^3-y^3\right)\\ =0+3x^2y+3xy^2=3x^2y+3xy^2\\ c,=x^3+1-x^2-x^3=1-x^2\\ d,=\left[\left(x+y\right)^2+z^2\right]=\left(x+y\right)^2+2z\left(x+y\right)+z^2\\ =x^2+y^2+z^2+2xy+2yz+2zx\)
a,=x4+2x2y+y2b,=[(y−x)3+(x−y)3]+[(x+y)3−x3−y3]=[−(x−y)3+(x−y)3]+(x3+3x2y+3xy2+y3−x3−y3)=0+3x2y+3xy2=3x2y+3xy2c,=x3+1−x2−x3=1−x2d,=[(x+y)2+z2]=(x+y)2+2z(x+y)+z2=x2+y2+z2+2xy+2yz+2zx