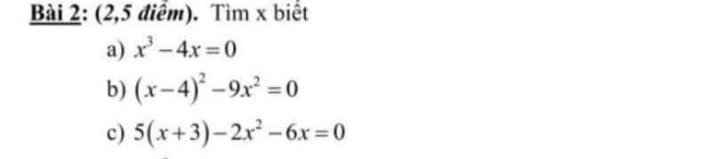Question

Answer 1

a) \(\Rightarrow x\left(x^2-4\right)=0\Rightarrow x\left(x-2\right)\left(x+2\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)

b) \(\Rightarrow\left(x-4-3x\right)\left(x-4+3x\right)=0\)

\(\Rightarrow-8\left(x+2\right)\left(x-1\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)

c) \(\Rightarrow5\left(x+3\right)-2x\left(x+3\right)=0\Rightarrow\left(x+3\right)\left(5-2x\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=-3\\x=\dfrac{5}{2}\end{matrix}\right.\)

Answer 2

   a) x³-4x=0

⇔x(x²-4)=0

⇔x(x-2)(x+2)=o

⇔x=0

      x-2=0⇔x=2

      x+2=0⇔x=-2

Vậy x ϵ {0;2;-2}

b) (x-4)²-9x²=0

   ⇔ (x-4)²-(3x)²=0

    ⇔ (x-4-3x)(x-4+3x)=0

    ⇔(-2x-4)(4x+4)=0

    ⇔-2x-4=0⇔x=-2

        4x+4=0⇔x=-1

Vậy x ϵ {-2;-1}

c) 5(x+3)-2x²-6x=0

⇔5(x+3)-2x(x+3)=0

⇔(x+3)(5-2x)=0

⇔x+3=0⇔x=-3

   5-2x=0⇔x=5/2

Vậy x ϵ {-3;5/2}