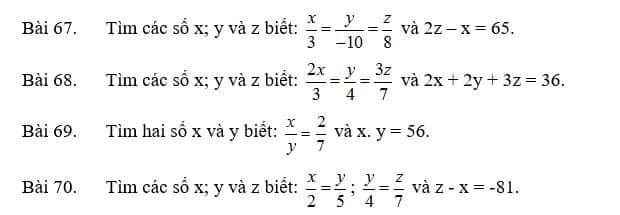\(\dfrac{x}{3}=\dfrac{y}{-10}=\dfrac{z}{8}\)
⇒ \(\dfrac{x}{3}=\dfrac{2z}{16}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{3}=\dfrac{2z}{16}=\dfrac{2z-x}{16-3}=\dfrac{65}{13}=5\)
⇒\(\left\{{}\begin{matrix}x=5.3=15\\y=5.-10=-50\\z=5.8=40\end{matrix}\right.\)
Bài 67
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{-10}=\dfrac{z}{8}=\dfrac{2z-x}{2\cdot8-3}=\dfrac{65}{13}=5\)
Do đó: x=15; y=-50; z=40
Bài 68: \(\dfrac{2x}{3}=\dfrac{y}{4}=\dfrac{3z}{7}\)
⇒\(\dfrac{2x}{3}=\dfrac{2y}{8}=\dfrac{3z}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{2x}{3}=\dfrac{2y}{8}=\dfrac{3z}{7}=\dfrac{2x+2y+3z}{3+8+7}=\dfrac{36}{18}=2\)
⇒\(\left\{{}\begin{matrix}x=3\\y=8\\z=\dfrac{14}{3}\end{matrix}\right.\)
Bài 69: \(\dfrac{x}{y}=\dfrac{2}{7}\)
⇒\(\dfrac{x}{2}=\dfrac{y}{7}\)
Đặt \(\dfrac{x}{2}=\dfrac{y}{7}=k\)
⇒ x=2k; y=7k
Thay vào:
⇒\(2k.7k=56\)
⇒ \(k^2=4\)
⇒ \(\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\)
Còn lại bạn thay vào là được