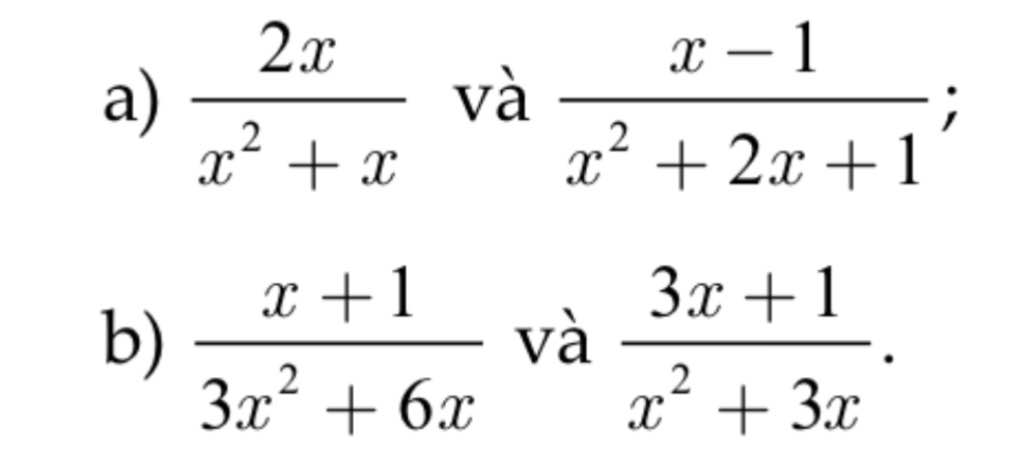1) \(\left\{{}\begin{matrix}\dfrac{2x}{x^2+x}=\dfrac{2x}{x\left(x+1\right)}=\dfrac{2x\left(x+1\right)}{x\left(x+1\right)^2}=\dfrac{2x^2+2x}{x\left(x+1\right)^2}\\\dfrac{x-1}{x^2+2x+1}=\dfrac{x-1}{\left(x+1\right)^2}=\dfrac{x\left(x-1\right)}{x\left(x+1\right)^2}=\dfrac{x^2-x}{x\left(x+1\right)^2}\end{matrix}\right.\)
2) \(\left\{{}\begin{matrix}\dfrac{x+1}{3x^2+6x}=\dfrac{x+1}{3x\left(x+2\right)}=\dfrac{\left(x+3\right)\left(x+1\right)}{3x\left(x+2\right)\left(x+3\right)}=\dfrac{x^2+4x+3}{3x\left(x+2\right)\left(x+3\right)}\\\dfrac{3x+1}{x^2+3x}=\dfrac{3x+1}{x\left(x+3\right)}=\dfrac{\left(3x+1\right).3\left(x+2\right)}{3x\left(x+2\right)\left(x+3\right)}=\dfrac{9x^2+21x+6}{3x\left(x+2\right)\left(x+3\right)}\end{matrix}\right.\)