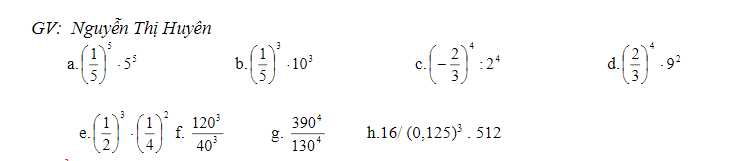\(a,=\left(\dfrac{1}{5}\cdot5\right)^5=1^5=1\\ b,=\left(\dfrac{1}{5}\cdot10\right)^3=2^3=8\\ c,=\left(-\dfrac{2}{3}:2\right)^4=\left(-\dfrac{1}{3}\right)^4=\dfrac{1}{81}\\ d,=\left(\dfrac{2}{3}\cdot3\right)^4=2^4=16\\ e,=\left(\dfrac{1}{2}\right)^3\cdot\left(\dfrac{1}{2}\right)^4=\left(\dfrac{1}{2}\right)^7=\dfrac{1}{128}\\ f,=\dfrac{40^3\cdot3^3}{40^3}=27\\ g,=\dfrac{3^4\cdot130^4}{130^4}=81\\ h,=\dfrac{16}{\dfrac{1}{512}\cdot512}=\dfrac{16}{1}=16\)
a: \(\left(\dfrac{1}{5}\right)^2\cdot5^2=1\)
b: \(\left(\dfrac{1}{5}\right)^3\cdot10^3=2^3=8\)
c: \(\left(-\dfrac{2}{3}\right)^4:2^4=\dfrac{2^4}{3^4\cdot2^4}=\dfrac{1}{81}\)
d: \(\left(\dfrac{2}{3}\right)^4\cdot9^2=\dfrac{2^4}{3^4}\cdot3^4=16\)