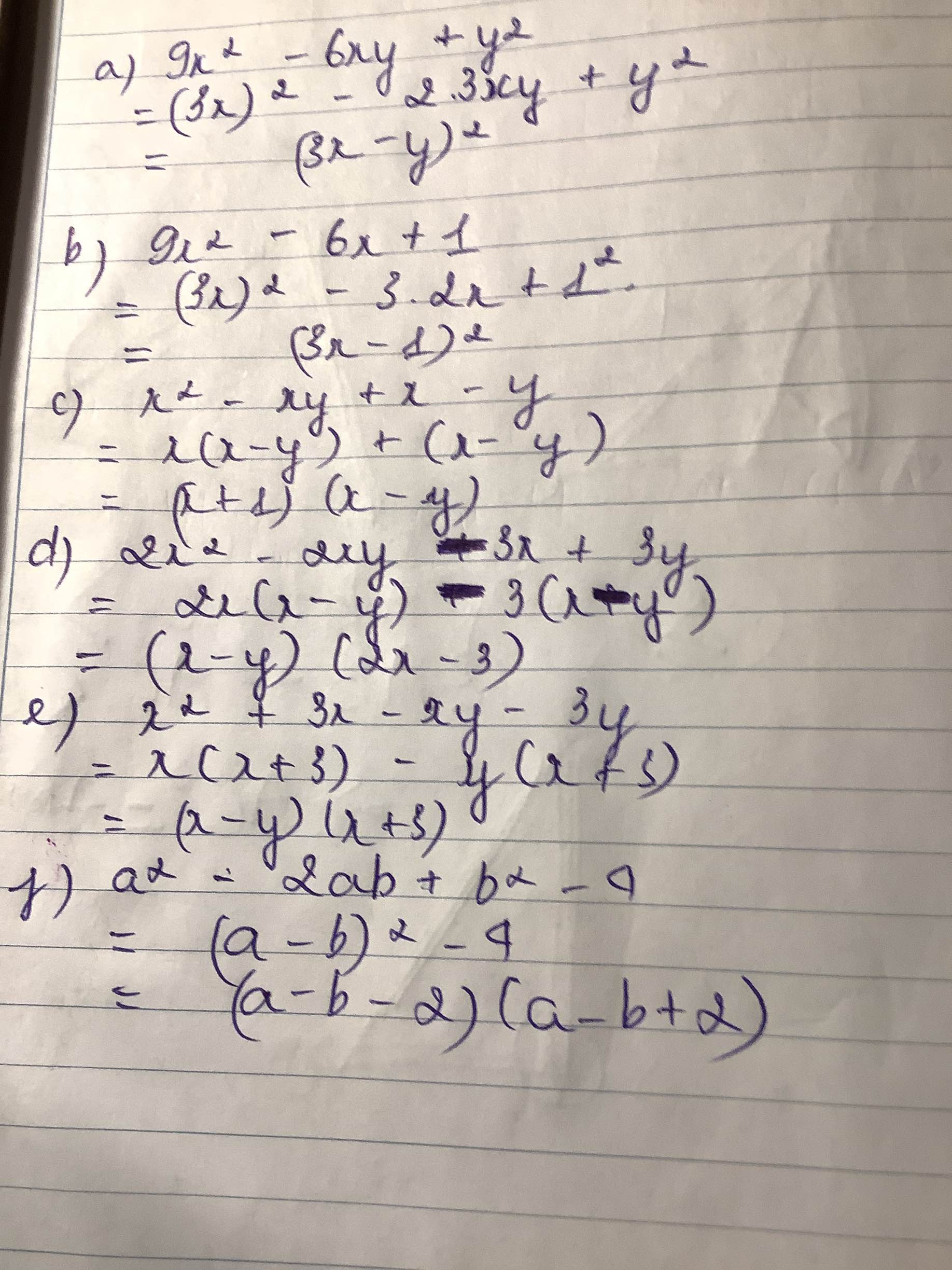a, \(9x^2-6xy+y^2\)
\(=\left(3x-y\right)^2\)
b, \(9x^2-6x+1\)
\(=\left(3x-1\right)^2\)
c, \(x^2-xy+x-y\)
\(=x^2+x-xy-y\\ =x\left(x+1\right)-y\left(x+1\right)\\ =\left(x-y\right)\left(x+1\right)\)
d, \(2x^2-2xy-3x+3y\)
\(=2x\left(x-y\right)-3\left(x-y\right)\\ =\left(2x-3\right)\left(x-y\right)\)
e, \(x^2+3x-xy-3y\)
\(=x\left(x+3\right)-y\left(x+3\right)\\ =\left(x-y\right)\left(x+3\right)\)
f, \(a^2-2ab+b^2-4\)
\(=\left(a-b\right)^2-2^2\\ =\left(a-b-2\right)\left(a-b+2\right)\)
a: \(9x^2-6xy+y^2=\left(3x-y\right)^2\)
b: \(9x^2-6x+1=\left(3x-1\right)^2\)
e: \(x^2-xy+x-y=\left(x-y\right)\left(x+1\right)\)
d: \(2x^2-2xy-3x+3y=\left(x-y\right)\left(2x-3\right)\)