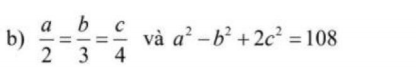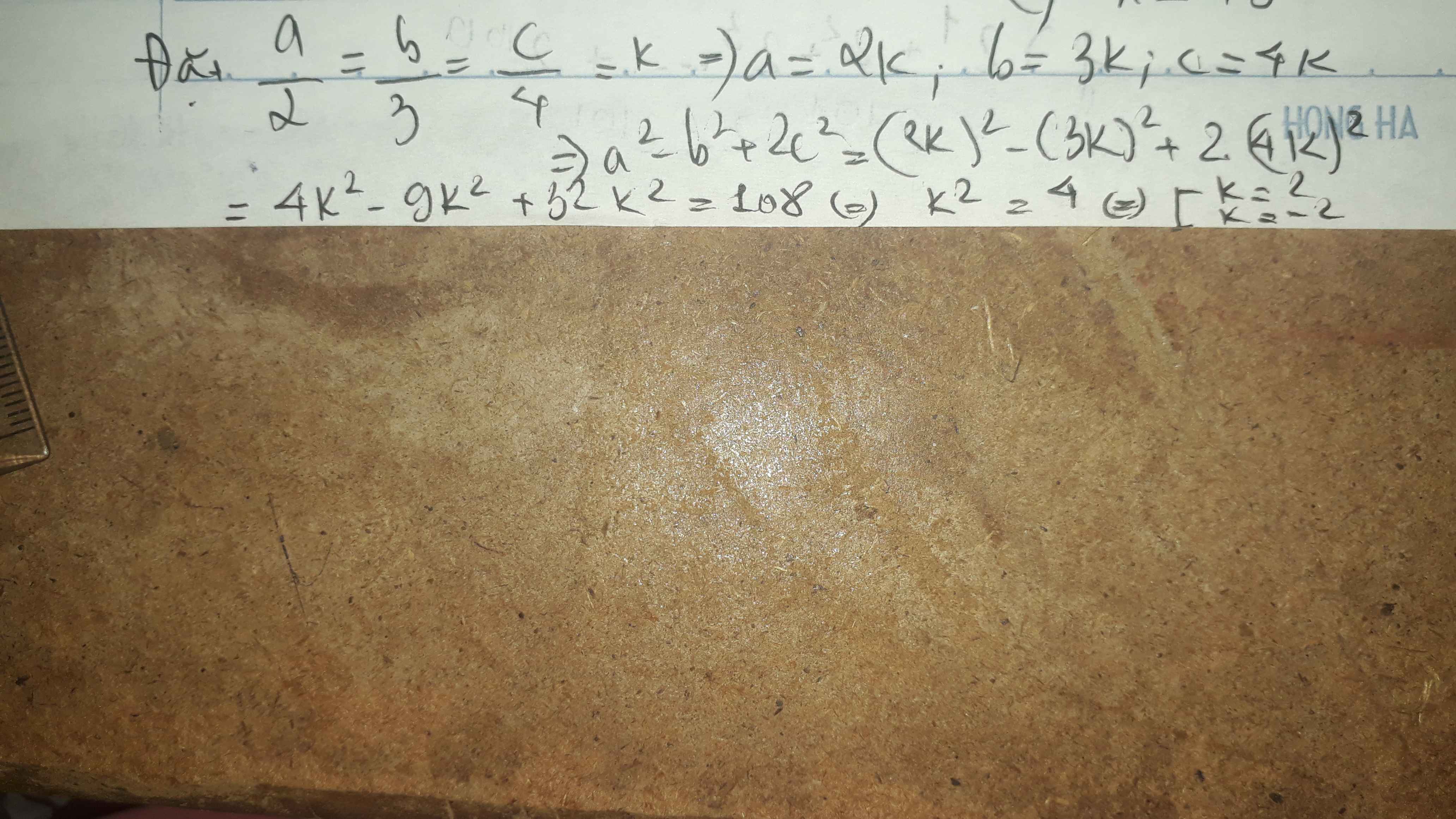Question

Answer 1

Answer 2

Đặt \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=k\)

\(\Leftrightarrow\left\{{}\begin{matrix}a=2k\\b=3k\\c=4k\end{matrix}\right.\)

Ta có: \(a^2-b^2+2c^2=108\)

\(\Leftrightarrow4k^2-9k^2+32k^2=108\)

\(\Leftrightarrow k^2=4\)

Trường hợp 1: k=2

\(\Leftrightarrow\left\{{}\begin{matrix}a=2k=4\\b=3k=6\\c=4k=8\end{matrix}\right.\)

Trường hợp 2: k=-2

\(\Leftrightarrow\left\{{}\begin{matrix}a=2k=-4\\b=3k=-6\\c=4k=-8\end{matrix}\right.\)