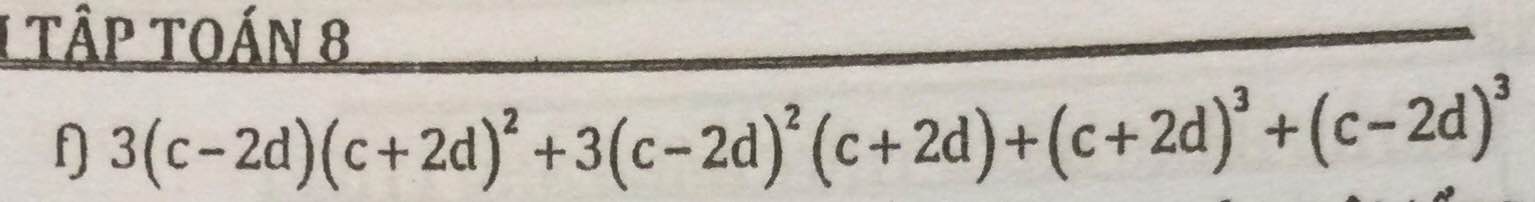f. \(3\left(c-ad\right)\left(c+2ad\right)^2+3\left(c-ad\right)^2\left(c+ad\right)+\left(c+ad\right)^3+\left(c-2d\right)^3\)
\(=\left(c-ad\right)^3+3\left(c-ad\right)^2\left(c+ad\right)+3\left(c-ad\right)\left(c+ad\right)^2+\left(c+ad\right)^3\)
\(=\left(c-ad+c+ad\right)^3=\left(2c\right)^3=8c^3\)
f: Ta có: \(3\left(c-2d\right)\left(c+2d\right)^2+3\left(c-2d\right)^2\cdot\left(c+2d\right)+\left(c+2d\right)^3+\left(c-2d\right)^3\)
\(=3\cdot\left(c^2-4d^2\right)\left(c+2d\right)+3\cdot\left(c^2-d^2\right)\cdot\left(c-2d\right)+\left(c+2d\right)^3+\left(c-2d\right)^3\)
\(=6c\left(c^2-4d^2\right)+c^3+6c^2d+12cd^2+8d^3+c^3-6c^2d+12cd^2-8d^3\)
\(=6c^3-24cd^2+2c^3+24cd^2\)
\(=8c^3\)