Question

Answer 1

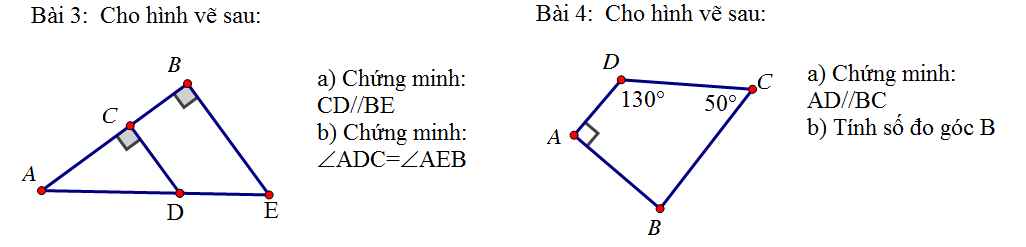
Bài 3:

a. Ta thấy:

$CD\perp AB$

$BE\perp AB$

$\Rightarrow CD\parallel BE$ (đpcm)

b. Vì $CD\parallel BE\Rightarrow \widehat{ADC}=\widehat{AEB}$ (hai góc ở vị trí đồng vị)

Answer 2

Bài 4:

a. Ta thấy:

$\widehat{ADC}+\widehat{DCB}=130^0+50^0=180^0$

Mà 2 góc này có vị trí trong cùng phía nên $AD\parallel BC$

b. Với $AD\parallel BC$

$\widehat{B}+\widehat{A}=180^0$ (hai góc trong cùng phía)

$\widehat{B}=180^0-\widehat{A}=180^0-90^0=90^0$

Answer 3

  a) ta có góc C=góc B =90 suy ra CD//BE ( hai góc đồng vị)

CD//BE suy ra góc ADC= góc AEB( đồng vị)

b) cách 1 ta có góc ADC+ góc DCB= 180 độ suy ra AD//BC( hai góc trong cùng phía bù nhau) 

Xát tứ giác ABCD có A+B+C+D= 360 độ

    Suy ra góc B= 360 -A-C-D

               Góc B= 360-90-50-130=90 độ

Cách 2 ta có AD//BC suy ra góc A + góc B = 180 ( hai góc trong cùng phía bù nhau)

Mà góc A bằng 90 độ suy ra góc B bằng 90 độ

 

Answer 4

Bài 3: 

a: Ta có: CD⊥AB

EB⊥AB

Do đó: CD//EB

b: Ta có: CD//EB

nên \(\widehat{ADC}=\widehat{AEB}\)

Answer 5

Bài 4:

a: Ta có: \(\widehat{D}+\widehat{C}=180^0\)

mà hai góc này là hai góc ở vị trí trong cùng phía

nên AD//CB

b: Ta có: AD//CB

nên \(\widehat{A}+\widehat{B}=180^0\)

hay \(\widehat{B}=90^0\)