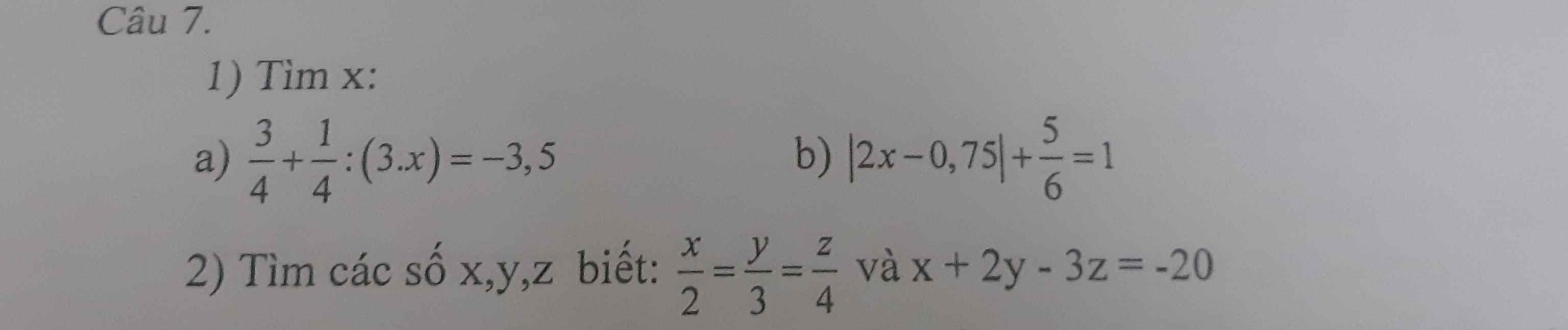a) Ta có: \(\dfrac{3}{4}+\dfrac{1}{4}:\left(3\cdot x\right)=-3.5\)
\(\Leftrightarrow\dfrac{1}{4}:\left(3x\right)=\dfrac{3}{4}+\dfrac{7}{2}=\dfrac{3}{4}+\dfrac{14}{4}=\dfrac{17}{4}\)
\(\Leftrightarrow3x=\dfrac{1}{4}:\dfrac{17}{4}=\dfrac{1}{17}\)
hay \(x=\dfrac{1}{51}\)
b) Ta có: \(\left|2x-0.75\right|+\dfrac{5}{6}=1\)
\(\Leftrightarrow\left|2x-\dfrac{3}{4}\right|=\dfrac{1}{6}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{3}{4}=\dfrac{1}{6}\\2x-\dfrac{3}{4}=-\dfrac{1}{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{11}{12}\\2x=\dfrac{7}{12}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11}{24}\\x=\dfrac{7}{24}\end{matrix}\right.\)
1)
\(\dfrac{3}{4}+\dfrac{1}{4}:\left(3.x\right)=-\dfrac{35}{10}\\ \dfrac{1}{4}:\left(3.x\right)=-\dfrac{35}{10}-\dfrac{3}{4}\)
\(\dfrac{1}{4}:\left(3.x\right)=-\dfrac{7}{2}-\dfrac{3}{4}\)
\(\dfrac{1}{4}:\left(3.x\right)=\dfrac{-17}{4}\\ 3.x=-\dfrac{17}{4}.\dfrac{1}{4}\\ 3x=\dfrac{-17}{16}\\ x=-\dfrac{17}{48}\)
2
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\\ \) với x+2y-3z
áp dụng...ta có
\(\dfrac{x}{2}=\dfrac{2y}{6}=\dfrac{3z}{12}\)=\(\dfrac{x+2y-3z}{2+6-12}=\dfrac{-20}{-4}=5\)
=>\(\dfrac{x}{2}=5\\ x=10\\ \dfrac{y}{3}=5\\ y=15\\ \dfrac{z}{4}=5\\ z=20\)
Bài 2:
Ta có: \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\)
nên \(\dfrac{x}{2}=\dfrac{2y}{6}=\dfrac{3z}{12}\)
mà x+2y-3z=-20
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{2y}{6}=\dfrac{3z}{12}=\dfrac{x+2y-3z}{2+6-12}=\dfrac{-20}{-4}=5\)
Do đó: \(\left\{{}\begin{matrix}x=10\\2y=30\\3z=60\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=10\\y=15\\z=20\end{matrix}\right.\)