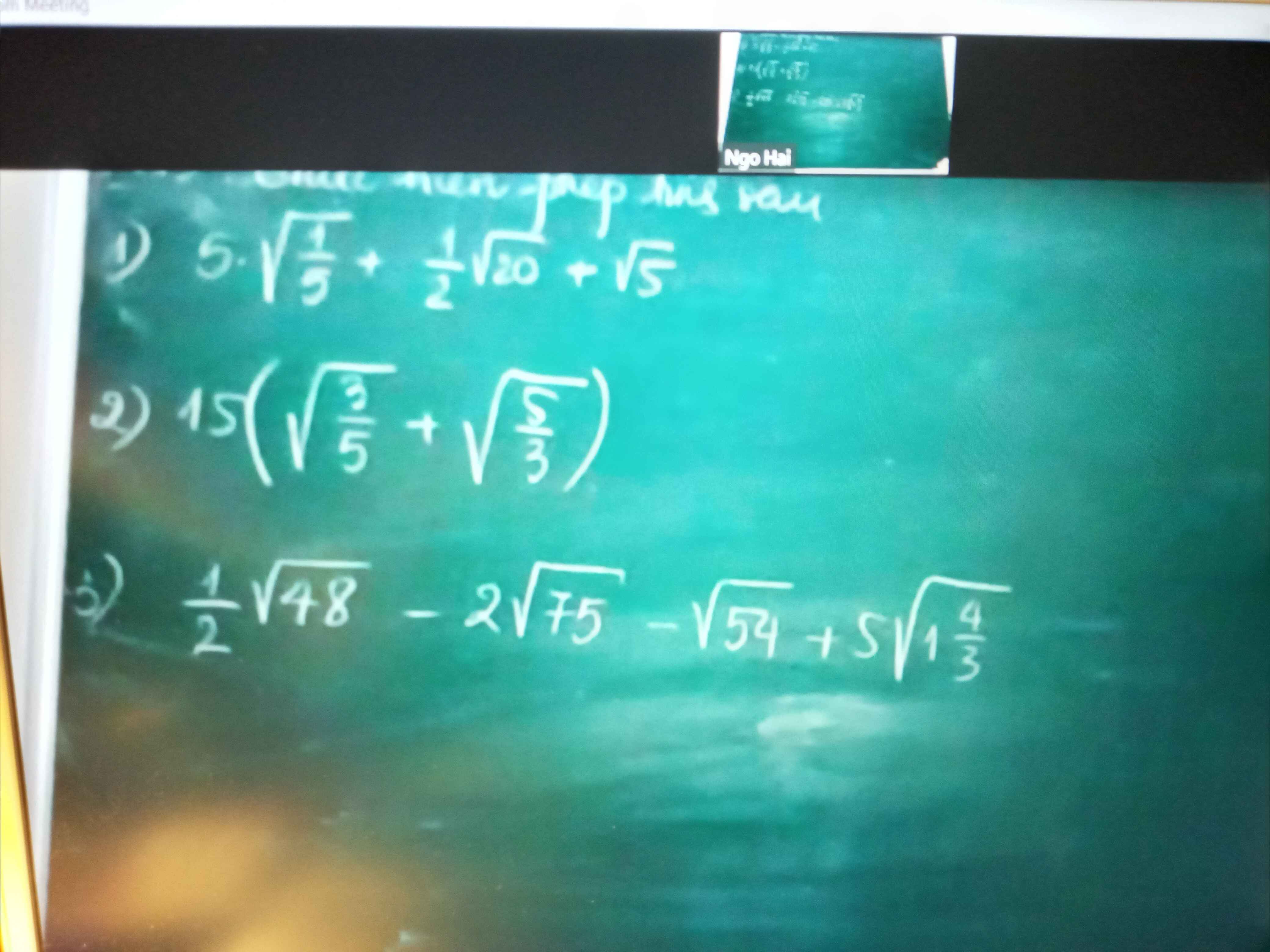
\(5.\sqrt{\dfrac{1}{5}}+\dfrac{1}{2}.\sqrt{20}+\sqrt{5}=5.\dfrac{1}{\sqrt{5}}+\dfrac{1}{2}.\sqrt{4}.\sqrt{5}+\sqrt{5}=\sqrt{5}+\dfrac{1}{2}.2.\sqrt{5}+\sqrt{5}=\sqrt{5}+\sqrt{5}+\sqrt{5}=3\sqrt{5}\)
\(15.\left(\sqrt{\dfrac{3}{5}}+\sqrt{\dfrac{5}{3}}\right)=15.\sqrt{\dfrac{3}{5}}+15.\sqrt{\dfrac{5}{3}}=15.\dfrac{\sqrt{3}}{\sqrt{5}}+15.\dfrac{\sqrt{5}}{\sqrt{3}}=\dfrac{\sqrt{5}.\sqrt{5}.3.\sqrt{3}}{\sqrt{5}}+\dfrac{\sqrt{3}.\sqrt{3}.5.\sqrt{5}}{\sqrt{3}}=\sqrt{5}.3.\sqrt{3}+\sqrt{3}.5.\sqrt{5}=3.\sqrt{15}+5.\sqrt{15}=8\sqrt{15}\)
Đúng 1
Bình luận (0)
