Viết phương trình đường tròn (C) qua điểm A(5;3) và tiếp xúc với đường thẳng (d): \(x+3y+2=0\) tại điểm B(1;-1).
\(x^2+y^2+4x+4y+2=0\) \(x^2+y^2+4x+4y-2=0\) \(x^2+y^2-4x-4y+2=0\) \(x^2+y^2-4x-4y-2=0\) Hướng dẫn giải: 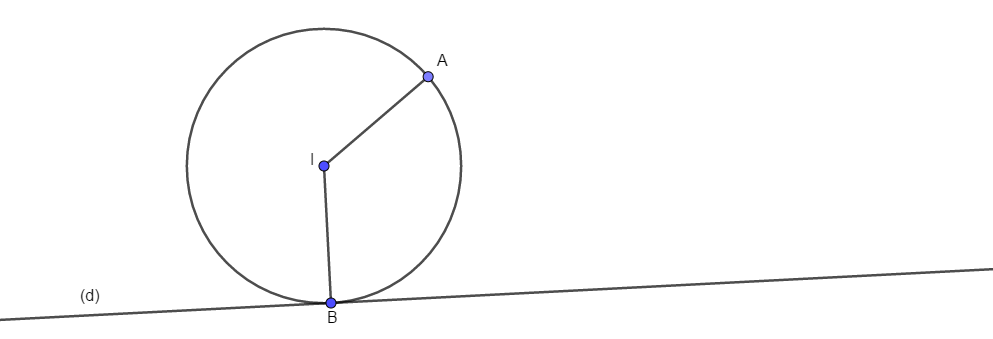
Đường thẳng (d): \(x+3y+2=0\) có vecto pháp tuyến \(\overrightarrow{n}\left(1;3\right)\) nên có vecto chỉ phương \(\overrightarrow{u}\left(3;-1\right)\). Kí hiệu \(\left(a;b\right)\) là tọa độ tâm I của (C). Từ giả thiết suy ra \(\overrightarrow{BI}.\overrightarrow{v}=0\) và \(IB=IA\) tức là
\(\left\{{}\begin{matrix}\left(a-1;b+1\right)\left(3;-1\right)=0\\\left(a-1\right)^2+\left(b+1\right)^2=\left(a-5\right)^2+\left(b-3\right)^2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}3\left(a-1\right)+\left(b+1\right).\left(-1\right)=0\\-2a+2b+2-10a-6b+34\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3a-b=4\\8a+8b=32\end{matrix}\right.\)
Giải hệ trên ta được \(a=b=2\). Như vậy I(2;2) và \(R^2=IA^2=\left(2-1\right)^2+\left(2+1\right)^2=10\). Phương trình của (C) là \(\left(x-2\right)^2+\left(y-2\right)^2=10\Leftrightarrow x^2+y^2-4x-4y-2=0\)

