Gọi O, G, H lần lượt là tâm đường tròn ngoại tiếp, trọng tâm, trực tâm tam giác ABC. Mệnh đề nào sau đây đúng?
\(\overrightarrow{OH}=\dfrac{3}{2}\overrightarrow{OG}\) \(\overrightarrow{OH}=3\overrightarrow{OG}\) \(\overrightarrow{OG}=\dfrac{1}{2}\overrightarrow{GH}\) \(\overrightarrow{OG}=\dfrac{3}{2}\overrightarrow{OH}\) Hướng dẫn giải: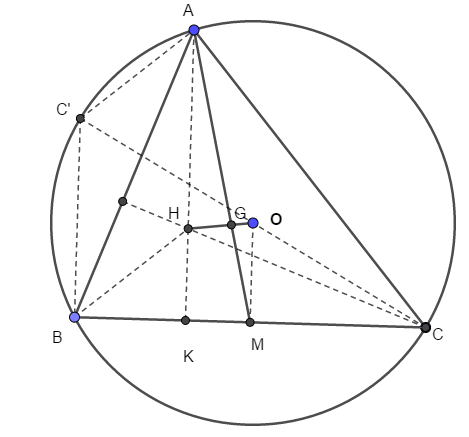
Với các kí hiệu như hình vẽ ta thấy AC'BH là hình bình hành, OM là đường trung bnhf tam giác CC'B nên \(\overrightarrow{OM}=\dfrac{1}{2}\left|\overrightarrow{C'B}\right|=\dfrac{1}{2}\overrightarrow{AH}\)\(\Rightarrow\overrightarrow{HG}=2\overrightarrow{GO}\)\(\Rightarrow\overrightarrow{OG}-\overrightarrow{OH}=-2\overrightarrow{OG}\Rightarrow\overrightarrow{OH}=3\overrightarrow{OG}\)

