
c: Coi hai chữ số 2 và 3 là một chữ số
=>Chúng ta sẽ cần tìm xem có bao nhiêu số có 4 chữ số khác nhau mà trong đó phải có chữ số {2;3}
Số cách chọn cho 3 chữ số còn lại là: \(5\cdot4\cdot3=60\left(cách\right)\)
Số cách xếp 2 chữ số 2 và 3 là 2(cách)
Do đó: Có \(60\cdot2=120\left(cách\right)\)
a; Gọi số lập được có dạng là \(\overline{abcde}\)
a có 7 cách chọn
b có 6 cách chọn
c có 5 cách chọn
d có 4 cách chọn
e có 3 cách chọn
Do đó: Có \(7\cdot6\cdot5\cdot4\cdot3=2520\left(số\right)\)
b: Gọi số lập được có dạng là \(\overline{abcdef}\)
f có 1 cách chọn
a có 6 cách chọn
b có 5 cách chọn
c có 4 cách chọn
d có 3 cách chọn
e có 2 cách chọn
Do đó: Có \(1\cdot2\cdot3\cdot4\cdot5\cdot6=720\left(cách\right)\)
Đúng 1
Bình luận (0)

Câu 7.
Từ các số 0, 1, 2, 3, 4, 5, 6, 7, 8. Hỏi có thể lập được bao nhiêu số tự nhiên biết:
a) Số có 4 chữ số b) Số có 5 chữ số khác nhau
c) Số chẵn có 5 chữ số d) Số chẵn có 6 chữ số khác nhau
e) Số lẻ có 6 chữ số khác nhau f) Số có 5 chữ số khác nhau và chia hết cho 5.
a: Gọi số lập được có dạng là \(\overline{abcd}\)
a có 8 cách chọn
b có 9 cách chọn
c có 9 cách chọn
d có 9 cách chọn
Do đó: Có \(8\cdot9\cdot9\cdot9=5832\left(cách\right)\)
b: Gọi số lập được có dạng là \(\overline{abcde}\)
a có 8 cách chọn
b có 8 cách chọn
c có 7 cách chọn
d có 6 cách chọn
e có 5 cách chọn
Do đó: Có \(8\cdot8\cdot7\cdot6\cdot5=13440\left(cách\right)\)
c: Gọi số lập được có dạng là \(\overline{abcde}\)
a có 8 cách chọn
b có 9 cách chọn
c có 9 cách chọn
d có 9 cách chọn
e có 5 cách chọn
Do đó: Có \(8\cdot9\cdot9\cdot9\cdot5=29160\left(cách\right)\)
d: Gọi số lập được có dạng là \(\overline{abcdef}\)
TH1: f\(\ne\)0
f có 4 cách chọn
a có 7 cách chọn
b có 7 cách chọn
c có 6 cách chọn
d có 5 cách chọn
e có 4 cách chọn
Do đó: Có \(4\cdot7\cdot7\cdot6\cdot5\cdot4=23520\left(cách\right)\)
TH2: f=0
a có 8 cách chọn
b có 7 cách chọn
c có 6 cách chọn
d có 5 cách chọn
e có 4 cách chọn
Do đó: Có \(8\cdot7\cdot6\cdot5\cdot4=6720\left(cách\right)\)
Tổng số cách là 6720+23520=30240(cách)
e: Gọi số lập được có dạng là \(\overline{abcdef}\)
f có 4 cách chọn(Các số có thể chọn là 1;3;5;7)
a có 7 cách chọn
b có 7 cách chọn
c có 6 cách chọn
d có 5 cách chọn
e có 4 cách chọn
Do đó: Có \(4\cdot7\cdot7\cdot6\cdot5=5880\left(cách\right)\)
f: Gọi số lập được có dạng là \(\overline{abcde}\)
Vì \(\overline{abcde}⋮5\) nên \(e\in\left\{0;5\right\}\)
TH1: e=0
a có 8 cách chọn
b có 7 cách chọn
c có 6 cách chọn
d có 5 cách chọn
Do đó: Có \(8\cdot7\cdot6\cdot5=1680\left(cách\right)\)
TH2: e=5
a có 7 cách chọn
b có 7 cách chọn
c có 6 cách chọn
d có 5 cách chọn
Do đó: Có \(7\cdot7\cdot6\cdot5=1470\left(cách\right)\)
Tổng số cách là 1680+1470=3150(cách)
Đúng 0
Bình luận (0)

Câu 6.
Từ các số 1,2,3,4,5,6,7 lập được bao nhiêu số tự nhiên gồm 4 chữ số khác nhau và là:
a) Số chẵn b) Số lẻ
c) Số chia hết cho 5 d) Tổng hai chữ số đầu bằng tổng hai chữ số cuối.
a: Gọi số lập được có dạng là \(\overline{abcd}\)
d có 3 cách chọn
a có 6 cách chọn
b có 5 cách chọn
c có 4 cách chọn
Do đó: Có \(3\cdot6\cdot5\cdot4=360\left(cách\right)\)
b: Gọi số lập được có dạng là \(\overline{abcd}\)
d có 4 cách chọn
a có 6 cách chọn
b có 5 cách chọn
c có 4 cách chọn
Do đó: Có \(4\cdot6\cdot5\cdot4=480\left(cách\right)\)
c: Gọi số lập được có dạng là \(\overline{abcd}\)
d có 1 cách chọn
a có 6 cách chọn
b có 5 cách chọn
c có 4 cách chọn
Do đó: Có \(6\cdot5\cdot4\cdot1=120\left(cách\right)\)
d: Các cặp số mà tổng hai chư số đầu bằng tổng hai chữ số cuối là:
{(1;7);(2;6)}; {(1;6);(2;5)}; {(1;5);(2;4)}; {(1;4);(2;3)}; {(2;6);(3;5)}; {(2;5); (3;4)}
=>Có 6 cặp
Với mỗi cặp, ta có số cách tráo hai chữ số lại là \(2!=2\left(cách\right)\)
=>Với 2 cặp (1;7); (2;6) ta có 2 cách hoán đổi vị trí hai cặp với nhau và với mỗi bộ số, ta lại có 2 cách hoán đổi vị trí
Do đó: Có \(2\cdot2\cdot2=8\left(cách\right)\)
=>Có tất cả là \(8\cdot6=48\left(cách\right)\)
Đúng 0
Bình luận (0)
Câu 5:
a, Số cách chọn một bạn phụ trách quỹ lớp: `18+12=40(\text{cách})`
b, Số cách chọn hai bạn, 1 bạn nam và nữ: `18*12=216(\text{cách})`
Đúng 0
Bình luận (2)
Cho hàm số y=-2x^2+x+3 có đồ thị là một Parabol (P).Vẽ đồ thị và xác định các khoảng đồng biến-nghịch biến của hàm số trên.Giúp m vs mai m thi r.Bạn nào giải nhớ vẽ hình hộ m nhá.M cảm ơn.
\(y=-2x^2+x+3\)
\(\left(P\right)\) đạt cực đại tại điểm \(\left(\dfrac{1}{4};\dfrac{25}{8}\right)=\left(0,25;3,125\right)\)
\(\Rightarrow\left(P\right)\) đồng biến trên \(\left(-\infty;\dfrac{1}{4}\right)\) và nghịch biến trên \(\left(\dfrac{1}{4};+\infty\right)\)
Đúng 1
Bình luận (1)
Cho hai đường thẳng d1: 3x-y+1=0 và d2: x-2y+2=0.
Gọi d3 là đường thẳng vuông góc với d1 và lần lượt cắt hai đường thẳng d1,d2 tại A và C, ta được diện tích tam giác ABC bằng 5.
Khi đó, phương trình tổng quát của đường thẳng d3 có dạng?
\(\left(d_1\right):3x-y+1=0\Rightarrow\overrightarrow{n_{PT}}=\left(3;-1\right)\)
\(\left(d_1\right)\perp\left(d_3\right)\Rightarrow\left(d_3\right):x+3y+c=0\)
\(\left(d_3\right)\cap\left(d_1\right)=A\left(x_A;y_A\right)\) là nghiệm hpt \(\left\{{}\begin{matrix}3x-y+1=0\\x+3y+c=0\end{matrix}\right.\)
\(\Rightarrow A\left(\dfrac{-3-c}{10};\dfrac{1-3c}{10}\right)\)
\(\left(d_3\right)\cap\left(d_2\right)=C\left(x_C;y_C\right)\) là nghiệm hpt \(\left\{{}\begin{matrix}x-2y+2=0\\x+3y+c=0\end{matrix}\right.\)
\(\Rightarrow C\left(\dfrac{-6-2c}{5};\dfrac{-4+c}{5}\right)\)
\(\left(d_1\right)\cap\left(d_2\right)=B\left(x_B;y_B\right)\) là nghiệm hpt \(\left\{{}\begin{matrix}3x-y+1=0\\x-2y+2=0\end{matrix}\right.\)
\(\Rightarrow B\left(0;1\right)\)
\(AC=\sqrt{\left(\dfrac{-3-c}{10}+\dfrac{6+2c}{5}\right)^2+\left(\dfrac{1-3c}{10}+\dfrac{4-c}{5}\right)^2}\)
\(\Rightarrow AC=\dfrac{1}{10}\sqrt{\left(9+3c\right)^2+\left(9-5c\right)^2}\)
Tương tự \(AB=\dfrac{1}{10}\sqrt{\left(c+3\right)^2+\left(9+3c\right)^2}\)
\(S_{ABC}=\dfrac{1}{2}.AC.AB=5\)
\(\Leftrightarrow\dfrac{1}{2}.\dfrac{1}{10}\sqrt{\left(9+3c\right)^2+\left(9-5c\right)^2}.\dfrac{1}{10}\sqrt{\left(c+3\right)^2+\left(9+3c\right)^2}=5\)
\(\Leftrightarrow\sqrt{\left(9+3c\right)^2+\left(9-5c\right)^2}.\sqrt{\left(c+3\right)^2+\left(9+3c\right)^2}=1000\)
Sau khi giải phương trình trên, ta được \(c=7;c=-13\)
Vậy phương trình tổng quát của \(\left(d_3\right):\left[{}\begin{matrix}x+3y+7=0\\x+3y-13=0\end{matrix}\right.\)
Đúng 1
Bình luận (3)
Từ các chữ số 0,1, 2, 3, 5 , có thể lập được bao nhiêu số tự nhiên gồm bốn chữ số đôi một khác nhau và không chia hết cho 5? A. 120 số.B. 72 số. C. 69 số.D. 54 số.
Đọc tiếp
Từ các chữ số 0,1, 2, 3, 5 , có thể lập được bao nhiêu số tự nhiên gồm bốn chữ số đôi một khác nhau và không chia hết cho 5?
| A. 120 số. | B. 72 số. |
|
| C. 69 số. | D. 54 số. |
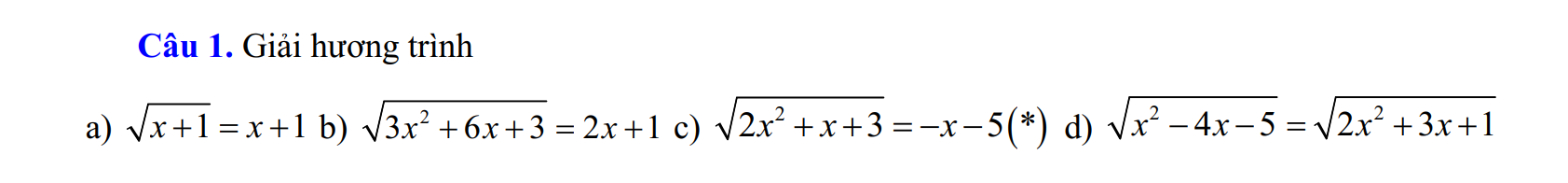
Câu 1. Giải phương trình
a) \(\sqrt{x+1} = x+1\)
b) \(\sqrt{3x^2 + 6x + 3} = 2x + 1\)
c) \(\sqrt{2x^2 + x + 3} = -x - 5\)
d) \(\sqrt{x^2 - 4x - 5} = \sqrt{2x^2 + 3x + 1}\)
a) \(\sqrt{x+1}=x+1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+1\ge0\\x+1=\left(x+1\right)^2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x\left(x+1\right)=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
b) \(\sqrt{3x^2+6x+3}=2x+1\)
\(\Leftrightarrow\sqrt{3\left(x^2+2x+1\right)}=2x+1\)
\(\Leftrightarrow\sqrt{3}\left|x+1\right|=2x+1\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{3}\left(x+1\right)=2x+1\\\sqrt{3}\left(x+1\right)=-2x-1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left(2-\sqrt{3}\right)x=\sqrt{3}-1\\\left(2+\sqrt{3}\right)x=-\sqrt{3}-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{3}-1}{2-\sqrt{3}}\\x=\dfrac{-\sqrt{3}-1}{2+\sqrt{3}}\end{matrix}\right.\)
c) \(\sqrt{2x^2+x+3}=-x-5\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x-5\ge0\\2x^2+x+3=\left(-x-5\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-5\\2x^2+x+3=x^2+10x+25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-5\\x^2-9x-22=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-5\\x=-2\cup x=11\end{matrix}\right.\) \(\Leftrightarrow x=-2\)
d) \(\sqrt{x^2-4x-5}=\sqrt{2x^2+3x+1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-4x-5\ge0\\x^2-4x-5=2x^2+3x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-1\cup x\ge5\\x^2-7x+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-1\cup x\ge5\\x=1\cup x=6\end{matrix}\right.\) \(\Leftrightarrow x=6\)
Đúng 0
Bình luận (0)

Câu 2.
Tìm các giá trị của tham số \( m \) để
a) \( f(x) = (m+1)x^2 + 5x + 2 \) là tam thức bậc hai không đổi dấu trên \(\mathbb{R}\);
b) \( f(x) = mx^2 - 7x + 4 \) là tam thức bậc hai âm với mọi \( x \in \mathbb{R}\);
c) \( f(x) = 3x^2 - 4x + (3m-1) \) là tam thức bậc hai dương với mọi \( x \in \mathbb{R}\);
d) \( f(x) = (m^2+1)x^2 - 3mx + 1 \) là tam thức bậc hai âm với mọi \( x \in \mathbb{R}\).
a) Để \(f\left(x\right)\) là tam thức bậc hai không đổi dấu \(\forall x\in R\)
\(\Leftrightarrow\left\{{}\begin{matrix}m+1\ne0\\\Delta=25-8\left(m+1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\8m>17\end{matrix}\right.\) \(\Leftrightarrow m>\dfrac{17}{8}\)
b) Để \(f\left(x\right)< 0,\forall x\in R\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\Delta=49-16m< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\m>\dfrac{49}{16}\end{matrix}\right.\) \(\Leftrightarrow m\in\varnothing\)
c) Để \(f\left(x\right)>0;\forall x\in R\)
\(\Leftrightarrow\left\{{}\begin{matrix}3>0\left(đúng\right)\\\Delta'=4-9m+3< 0\end{matrix}\right.\) \(\Leftrightarrow m>\dfrac{7}{9}\)
d) Để \(f\left(x\right)< 0,\forall x\in R\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2+1< 0\left(Sai\right)\\\Delta=9m^2-4m^2-4< 0\end{matrix}\right.\) \(\Leftrightarrow m\in\varnothing\)
Đúng 1
Bình luận (0)
Cho △ 2x-y-3=0
a)Viết phương trình △1 qua A(-1,3) và //Δ
b)Viết phương trình △2 qua A và +△
c)Tìm A' đối xứng với A qua Δ
d) Cho P(2;-1) Tìm M ∈ △(MA,MB) min
a: Δ1//Δ
=>Δ1: 2x-y+c=0
Thay x=-1 và y=3 vào Δ1, ta được:
\(2\cdot\left(-1\right)-3+c=0\)
=>c-5=0
=>c=5
=>Δ1: 2x-y+5=0
b: Δ2\(\perp\)Δ
=>Δ2: x+2y+c=0
Thay x=-1 và y=3 vào Δ2, ta được:
-1+6+c=0
=>c+5=0
=>c=-5
=>Δ2: x+2y-5=0
c: A' đối xứng với A qua Δ
=>A'A\(\perp\)Δ tại trung điểm của A'A
mà A\(\in\)Δ2 và Δ2\(\perp\)Δ
nên giao điểm của Δ và Δ2 chính là trung điểm của A'A
Tọa độ giao điểm của Δ và Δ2 là:
\(\left\{{}\begin{matrix}x+2y-5=0\\2x-y-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2y+5\\2\left(-2y+5\right)-y-3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-2y+5\\-4y+10-y-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2y+5\\-5y+7=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{7}{5}\\x=-2\cdot\dfrac{7}{5}+5=-\dfrac{14}{5}+5=\dfrac{11}{5}\end{matrix}\right.\)
Do đó, ta có:
\(\left\{{}\begin{matrix}x_{A'}+x_A=2\cdot\dfrac{11}{5}=\dfrac{22}{5}\\y_{A'}+y_A=2\cdot\dfrac{7}{5}=\dfrac{14}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_{A'}=\dfrac{22}{5}-\left(-1\right)=\dfrac{27}{5}\\y_{A'}=\dfrac{14}{5}-3=-\dfrac{1}{5}\end{matrix}\right.\)
=>A'(27/5;-1/5)
Đúng 0
Bình luận (0)














