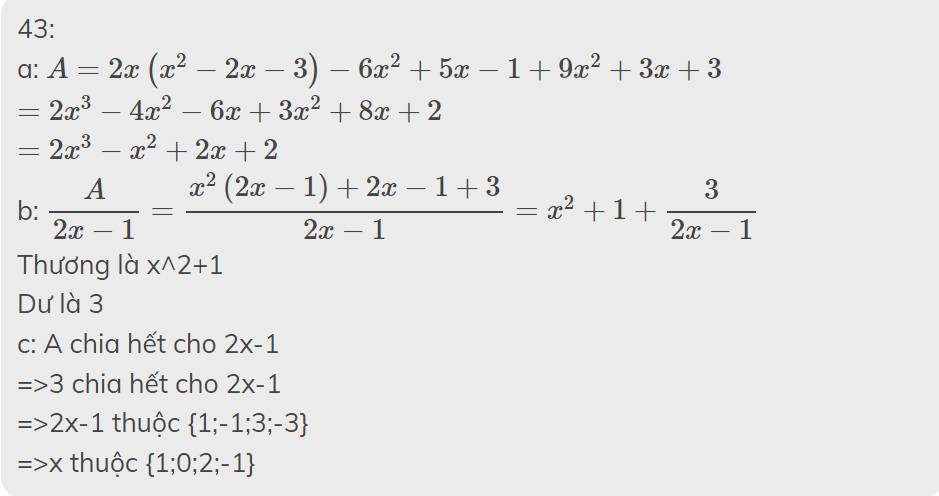Một bể cả đang chứa 150 lít nước, người ta cho hai vòi chảy vào bể, mỗi phút mỗi vòi cháy được x lít. Cùng lúc đó người ta tháo nước cũ trong bể cả ra bằng một vòi khác chảy nước từ bể ra ngoài. Mỗi phút lượng nước chảy ra bằng lượng nước chảy vào. Hãy viết biểu thức biểu thị lượng nước trong bể khi đồng thời mở cả các vòi trên sau 20 phút. (Có giải thích quá trình đưa ra biểu thức).
Chương IV : Biểu thức đại số
Một bể cả đang chứa 150 lít nước, người ta cho hai vòi chảy vào bể, mỗi phút mỗi vòi cháy được x lít. Cùng lúc đó người ta tháo nước cũ trong bể cả ra bằng một vòi khác chảy nước từ bể ra ngoài. Mỗi phút lượng nước chảy ra bằng lượng nước chảy vào. Hãy viết biểu thức biểu thị lượng nước trong bể khi đồng thời mở cả các vòi trên sau 20 phút. (Có giải thích quá trình đưa ra biểu thức).
Đọc tiếp
Sau 20 phút, lượng nước chảy vào bể là: 20 . 2x = 40x (l)
Sau 20 phút, lượng nước từ bể chảy ra ngoài là: 20x (l)
Biểu thức biểu thị lượng nước trong bể sau khi đồng thời mở các vòi trên sau 20 phút:
150 + 40x - 20x = 150 + 20x (l)
Đúng 0
Bình luận (0)
Bài 1. Cho các đơn thức sau:(1): 4𝑥𝑦; (2): − 4𝑥𝑦𝑧3; (3):13𝑥2𝑦; (4): √7𝑥𝑦; (5): 9𝑥𝑦𝑧3; (6): 𝑥𝑦;(7): 5𝑥𝑦2; (8): 𝑥3𝑦3𝑧; (9): 𝑥2𝑦; (10): 𝑥2; (11): 10𝑦; (12): −𝑥2.a) Đơn thức nào có bậc cao nhất, thấp nhất và có bậc bằng nhau?b) Những đơn thức nào đồng dạng với nhau?
Đọc tiếp
Bài 1. Cho các đơn thức sau:
(1): 4𝑥𝑦; (2): − 4𝑥𝑦𝑧3; (3):
1
3
𝑥2𝑦; (4): √7𝑥𝑦; (5): 9𝑥𝑦𝑧3; (6): 𝑥𝑦;
(7): 5𝑥𝑦2; (8): 𝑥3𝑦3𝑧; (9): 𝑥2𝑦; (10): 𝑥2; (11): 10𝑦; (12): −𝑥2
.
a) Đơn thức nào có bậc cao nhất, thấp nhất và có bậc bằng nhau?
b) Những đơn thức nào đồng dạng với nhau?
Bạn xem lại sao đề lỗi hiển thị như này nhở?
Đúng 3
Bình luận (0)
Câu 2: (1,0 điểm) Một hộp có 15 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1;2;3;...;13;14;15. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của các biến cố sau: a) A: “Rút được thẻ ghi số lẻ”: b) B: “Rút được thẻ ghi số chia hết cho 3"
a: A:"Rút được thẻ ghi số lẻ"
=>A={1;3;5;7;9;11;13;15}
=>n(A)=8
=>\(P\left(A\right)=\dfrac{8}{15}\)
b: B:"Rút được thẻ ghi số chia hết cho 3"
=>B={3;6;9;12;15}
=>n(B)=5
=>\(P\left(B\right)=\dfrac{5}{15}=\dfrac{1}{3}\)
Đúng 1
Bình luận (0)
43. Cho A = 2x(x + 1)(x-3)-(2x-1)(3x-1) + 3(3x² + x + 1).
a) Rút gọn biểu thức A.
b) Tìm thương và dư khi chia A cho 2x − 1.
c) Tìm giá trị nguyên của x để giá trị của biểu thức A chia hết cho giá trị của biểu thức 2x-1.
42. Cho A x² - 3x - 1, B 2x2-x-3, C 3x²+ 5x - 1.Tính A - B + C rồi tính giá trị của biểu thức với x 1 243. Cho A 2x(x + 1)(x-3)-(2x-1)(3x-1) + 3(3x² + x + 1).a) Rút gọn biểu thức A.b) Tìm thương và dư khi chia A cho 2x − 1.c) Tìm giá trị nguyên của x để giá trị của biểu thức A chia hết cho giá trị của biểu thức 2x-1.44. Tìm nghiệm của các đa thức :a) 3x-7;b) 2x² + 9;
Đọc tiếp
42. Cho A = x² - 3x - 1, B = 2x2-x-3, C= 3x²+ 5x - 1.
Tính A - B + C rồi tính giá trị của biểu thức với x = 1 2
43. Cho A = 2x(x + 1)(x-3)-(2x-1)(3x-1) + 3(3x² + x + 1).
a) Rút gọn biểu thức A.
b) Tìm thương và dư khi chia A cho 2x − 1.
c) Tìm giá trị nguyên của x để giá trị của biểu thức A chia hết cho giá trị của biểu thức 2x-1.
44. Tìm nghiệm của các đa thức :
a) 3x-7;
b) 2x² + 9;
\(Bài.44:\\ a,3x-7=0\\ \Leftrightarrow3x=7\\ \Leftrightarrow x=\dfrac{7}{3}\\ b.2x^2+9=0\\ \Leftrightarrow x^2=-\dfrac{9}{2}\left(vô.lí\right)\\ \Rightarrow Không.có.x.thoả.mãn\)
Đúng 1
Bình luận (0)
43:
a: \(A=2x\left(x^2-2x-3\right)-6x^2+5x-1+9x^2+3x+3\)
\(=2x^3-4x^2-6x+3x^2+8x+2\)
\(=2x^3-x^2+2x+2\)
b: \(\dfrac{A}{2x-1}=\dfrac{x^2\left(2x-1\right)+2x-1+3}{2x-1}=x^2+1+\dfrac{3}{2x-1}\)
Thương là x^2+1
Dư là 3
c: A chia hết cho 2x-1
=>3 chia hết cho 2x-1
=>2x-1 thuộc {1;-1;3;-3}
=>x thuộc {1;0;2;-1}
Đúng 1
Bình luận (0)
45. Thực hiện phép tính:
a) 5x6 : (-3x²);
c) (4x³-3x² + 2x) : 2x.
46. Rút gọn rồi tính giá trị của biểu thức A với x = −0,2.
A = (6x4 - 4x³ + 2x²): 2x² - (x-2)(3x-1).
47. Tìm x, biết (3x* – 6x3) : 2x3 = 6.
46:
\(A=\dfrac{2x^2\left(3x^2-2x+1\right)}{2x^2}-\left(3x^2-x-6x+2\right)\)
\(=3x^2-2x+1-3x^2+7x-2=5x-1\)
Khi x=-0,2 thì A=-1-1=-2
45:
a: \(=\dfrac{-5x^6}{3x^2}=-\dfrac{5}{3}x^4\)
c: \(=\dfrac{2x\left(2x^2-\dfrac{3}{2}x+1\right)}{2x}=2x^2-\dfrac{3}{2}x+1\)
Đúng 2
Bình luận (0)
giúp mình với ạ
25. Thực hiện phép tính :
a) (3x-1)(6x-1) 2x(9x-4);
b) (y-3)(y² + y + 1) − y(y² - 2).
26. Rút gọn biểu thức A rồi tính giá trị biểu thức với x = −2.
A = (2x-1)(6x + 5) - (4x + 1)(3x-2).
26:
A=12x^2+10x-6x-5-(12x^2-8x+3x-2)
=12x^2+4x-5-12x^2+5x+2
=9x-3
Khi x=-2 thì A=-18-3=-21
25:
b: \(\left(y-3\right)\left(y^2+y+1\right)-y\left(y^2-2\right)\)
=y^3+y^2+y-3y^2-3y-3-y^3+2y
=-2y^2-3
Đúng 1
Bình luận (0)
mong mng giúp mik bài này nhanh với ạ, mik đang rất cần gấp !! : 1 khu vườn HCN có chiều rộng x mét, chiều dài gấp đôi chiều rộng . ng ta đào 1 lối đi xung quanh khu vườn ( thuộc đất của vườn ) rộng 2 mét. tính diện tích còn lại của khu vườn bt x = 7 ( m )
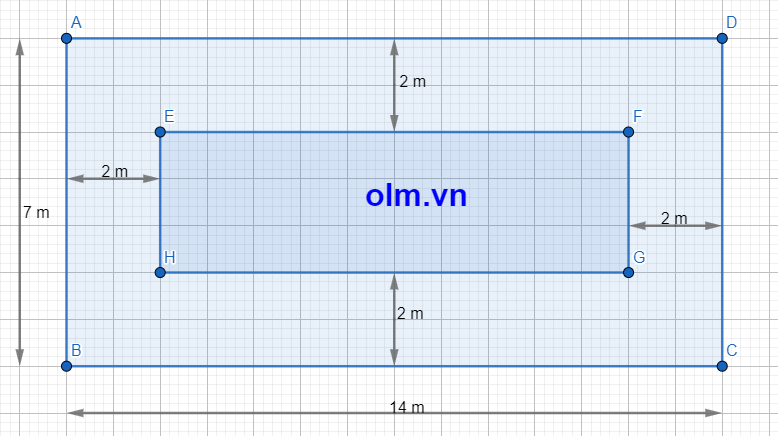
Chiều rộng khu vườn là: \(x\) (m); \(x>0\)
Chiều dài của khu vườn là: \(x\times\)2 = 2\(x\) (m)
Chiều dài còn lại của khu vườn sau khi mở lối đi là: 2\(x\) - (2 + 2) = \(2x-4\) (m)
Chiều rộng còn lại của khu vườn sau khi mở lối đi là: \(x-\left(2+2\right)\) = \(x-4\) (m)
Diện tích còn lại của khu vườn sau khi mở lối đi là: (\(2x-4\))(\(x-4\)) (m)(1)
Thay \(x\) = 7 m vào biểu thức (1) ta có:
Diện tích còn lại của khu vườn sau khi mở lối đi là:
(2.7 - 4)(7 - 4) = 30 (m2)
Kết luận: Diện tích còn lại của khu vườn sau khi mở lối đi là: 30 m2
Đúng 3
Bình luận (1)
Cho hai đa thức P(x) 5x3 – 3x + 7 – x và Q(x) -5x3 + 2x – 3 + 2x – x2– 2a. Thu gọn,sắp xếp theo lũy thừa giảm dần của biến hai đa thức P(x) và Q(x)b. Tìm đa thức M(x) P(x) + Q(x) và N(x) P(x) – Q(x)
Đọc tiếp
Cho hai đa thức P(x) = 5x3 – 3x + 7 – x và Q(x) = -5x3 + 2x – 3 + 2x – x2– 2
a. Thu gọn,sắp xếp theo lũy thừa giảm dần của biến hai đa thức P(x) và Q(x)
b. Tìm đa thức M(x) = P(x) + Q(x) và N(x) = P(x) – Q(x)
`a,`
`P(x)=5x^3 - 3x+7 -x`
`= 5x^3+(-3x-x)+7`
`= 5x^3-4x+7`
`b,`
`-5x^3+2x-3+2x-x^2-2`
`= -5x^3-x^2+(2x+2x)+(-3-2)`
`= -5x^3-x^2+4x-5`
`b,`
`M(x)=(5x^3-4x+7)+(-5x^3-x^2+4x-5)`
`= 5x^3-4x+7-5x^3-x^2+4x-5`
`= (5x^3-5x^3)-x^2+(-4x+4x)+(7-5)`
`= -x^2+2`
`N(x)=(5x^3-4x+7)-(-5x^3-x^2+4x-5)`
`= 5x^3-4x+7+5x^3+x^2-4x+5`
`= (5x^3+5x^3)+x^2+(-4x-4x)+(7+5)`
`= 10x^3+x^2-8x+12.`
Đúng 2
Bình luận (0)
a: P(x)=5x^3-4x+7
Q(x)=-5x^3-x^2+4x-5
b: M(x)=5x^3-4x+7-5x^3-x^2+4x-5=-x^2+2
N(x)=5x^3-4x+7+5x^3+x^2-4x+5=10x^3+x^2-8x+12
Đúng 0
Bình luận (0)
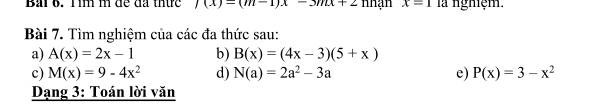
Cần gấp bài 7 ạ!
a: A(x)=0
=>2x-1=0
=>x=1/2
b: B(x)=0
=>(4x-3)(x+5)=0
=>x=3/4 hoặc x=-5
c: P(x)=0
=>3-x^2=0
=>x^2=3
=>\(x=\pm\sqrt{3}\)
d: M(x)=0
=>9-4x^2=0
=>4x^2=9
=>x=3/2 hoặc x=-3/2
e: N(a)=0
=>2a^2-3a=0
=>a=0; a=3/2
Đúng 1
Bình luận (0)