Toán lớp 10 vector
Cho tứ giác ABCD,
a) Tìm vị trí của M; N sao cho:
AM= AB + AC - BC
AN= AB - AC + AD
b) chứng minh : NM = AC + DB
Chương 1: VECTƠ
Hỏi đáp
Trong mp Oxy cho tam giác ABC có A(1;2), B(-2;-3), C(4;-1).
a. Tính độ dài đường cao AH của . Từ đó suy ra diện tích .
b. Tìm tọa độ tâm đường tròn ngoại tiếp
giúp mik đi
Cho tam giác ABC, tìm M sao cho:a, overrightarrow{MA}+2overrightarrow{MB}+3overrightarrow{MC} 0b, overrightarrow{MA}+2overrightarrow{MB}−4overrightarrow{MC} 0
Đọc tiếp
Cho tam giác ABC, tìm M sao cho:
a, \(\overrightarrow{MA}\)
b, \(\overrightarrow{MA}\)
a.Gọi E là trung điểm AC ; F là trung điểm BC
\(\overrightarrow{MA}+2\overrightarrow{MB}+3\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{MA}+\overrightarrow{MC}\right)+2\left(\overrightarrow{MB}+\overrightarrow{MC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow2\overrightarrow{ME}+4\overrightarrow{MF}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{ME}+2\overrightarrow{MF}=\overrightarrow{0}\)
Điểm M nằm trên đoạn EF sao cho \(\frac{MF}{ME}=\frac{1}{2}\)
Đúng 0
Bình luận (0)
đề bài có phải là
a. \(\overrightarrow{MA}+2\overrightarrow{MB}+3\overrightarrow{MC}=\overrightarrow{0}\)
b. \(\overrightarrow{MA}+2\overrightarrow{MB}-4\overrightarrow{MC}=\overrightarrow{0}\)
Đúng 0
Bình luận (1)
giúp mik với !!!! HELP
1.Cho tam giác ABC, gọi G là trọng tâm tam giác a.Gọi H là điểm đối xứng với G qua B. CMRvectơ HA - 5vectơ HB + vectơ HC vectơ 0.b.Gọi I và J là 2 điểm thoả mãn vectơ IA 2vectơ IB , 3vectơ JA + 2vectơ JC vectơ 0 . CM 3 điểm I,J,G thẳng hàng .2.Cho tam giác đều ABC tâm O. M là điểm bất kì trong tam giác . Hạ MD,ME,MF lần lượt vuông góc với các cạnh BC,CA,AB.CMR vectơ MD + vectơ ME + vectơ MF 3/2 vectơ MO
Đọc tiếp
1.Cho tam giác ABC, gọi G là trọng tâm tam giác
a.Gọi H là điểm đối xứng với G qua B. CMR
vectơ HA - 5vectơ HB + vectơ HC = vectơ 0.
b.Gọi I và J là 2 điểm thoả mãn vectơ IA = 2vectơ IB , 3vectơ JA + 2vectơ JC = vectơ 0 . CM 3 điểm I,J,G thẳng hàng .
2.Cho tam giác đều ABC tâm O. M là điểm bất kì trong tam giác . Hạ MD,ME,MF lần lượt vuông góc với các cạnh BC,CA,AB.CMR vectơ MD + vectơ ME + vectơ MF = 3/2 vectơ MO
điều kiện để 2 tam giác có cùng trọng tâm
giả sử tam giác ABC và A'B'C' lần lượt có trọng tâm là G, G'. hai tam giác cùng trọng tâm <=> '\(\overrightarrow{GG'}=0\) <=> \(\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}\)
Đúng 0
Bình luận (0)
cho tam giác OAB .giả sử
{vecto OA + vecto OB = vecto OM
{vecto OA -vecto OB= vecto ON
a, khi nào thì điểm M nằm trên đường phân giác trọng của góc AOB?
b, ,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,ngoài,,,,,,,,,,,,,,,,,,,,,,,,,,?
mình sửa lại ý
b, khi nào thì N nằm trên đường phân giác ngoài của góc AOB
Đúng 0
Bình luận (0)
Cho hình thoi ABCD tâm O, có cạnh bằng a, góc A 60 độ.
1. Tình \(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|\)
2. Tính \(\left|2\overrightarrow{OB}-3\overrightarrow{OC}\right|\)
Trên mặt phẳng cho 2013 vec-tơ trong đó không có hai vec-tơ nào cùng phương. Biết rằng tổng của 2012 vec-tơ bất kỳ đều cùng phương với vec-tơ còn lại. chứng minh rằng tổng của 2013 vec-tơ đó bằng 0.
Cho ba điểm A,B,C cố định thẳng hàng theo thứ tự đó. Đường tròn tâm O di động luôn đi qua B, C. kẻ qua A các tiếp tuyến AE, AF đến đường tròn tâm O. Gọi E,F là hai tiếp điểm . Gọi I là trung điểm của BC và K là giao của FI với đường tròn tâm O. CMR: véc tơ EK và véc tơ AB cùng phương
a) Vì tam giác AFB đồng dạng với ACF(g.g) nên:
AF/AC=AB/AF hay AF^2=AB.AC => AF=căn(AB.AC) ko đổi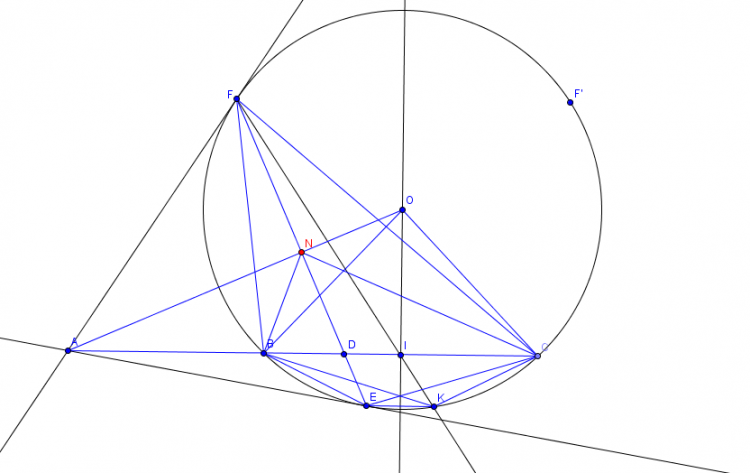 
Mà AE=AF (T/cTtuyen) nên E, F cùng thuộc đường tròn bán kính căn(AB.AC)
b)Ta có: OI vuông góc với BC (T/ đường kính và dây)
Các điểm E, F, I cùng nhìn OA dưới 1 góc ko đổi 90 độ nên O,I,F,A,E cùng thuộc đường tròn đường kính OA
Ta có góc FIA=FOA(Cùng chắn cung FA trong đường tròn (OIFAE)
Mà góc FKE=FOA( Cùng bằng \(\frac{1}{2}\) góc FOE)
Suy ra góc FIA=FKE, nhưng hai góc này lại ở vị trí SLT nên KE//AB
Đúng 0
Bình luận (1)