Bài 6: Ôn tập chương Vecơ trong không gian. Quan hệ vuông góc trong không gian.

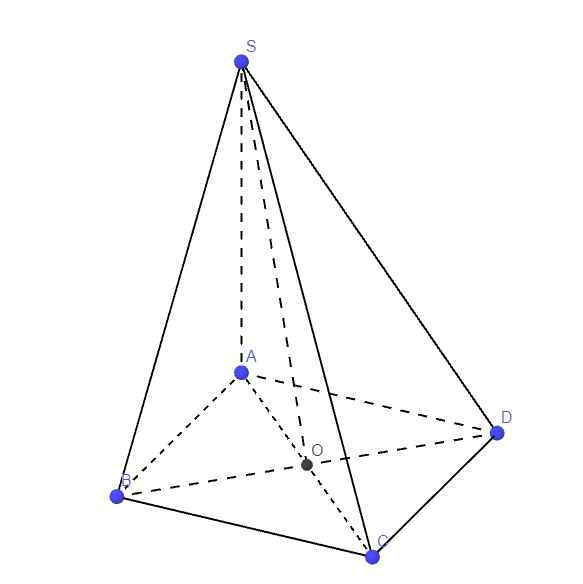
Chóp S.ABCD đều nên ABCD là HV \(\Rightarrow BD\perp AC\)  (1) 

 O = \(AC\cap BD\) . Dễ dàng c/m : BD \(\perp SO\) (2) 

Từ (1) ; (2) \(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp SA\)  \(\Rightarrow\left(SA;BD\right)=90^o\)

Chọn D 

a.

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)

b.

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\)  \(\Rightarrow BD\perp\left(SAC\right)\)

Mà \(SO\in\left(SAC\right)\Rightarrow BD\perp SO\)

c.

\(SA\perp\left(ABCD\right)\Rightarrow AO\) là hình chiếu vuông góc của SO lên (ABCD)

\(\Rightarrow\widehat{SOA}\) là góc giữa SO và (ABCD)

\(AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)

\(tan\widehat{SOA}=\dfrac{SA}{AO}=\sqrt{6}\Rightarrow\widehat{SOA}\approx67^047'\)

2

Đặt OA = a ; OB = b ; OC = c . Khi đó : 

\(OA+OB+OC+AB+BC+AC=a+b+c+\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{a^2+c^2}\)

AD BĐT Cauchy ta được : \(\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{a^2+c^2}\ge\sqrt{2}\left(a+b+c\right)\)

Suy ra : l \(\ge\left(\sqrt{2}+1\right)\left(a+b+c\right)\ge\left(\sqrt{2}+1\right)3\sqrt[3]{abc}\)

Có : \(V=V_{OABC}=\dfrac{abc}{6}\)  . Suy ra :   \(l\ge3\left(\sqrt{2}+1\right)\sqrt[3]{6V}\Leftrightarrow V\le\dfrac{l^3}{27\left(\sqrt{2}+1\right)^3.6}=\dfrac{l^3}{162\left(\sqrt{2}+1\right)^3}\)

" = " \(\Leftrightarrow a=b=c\) = \(\dfrac{l\left(\sqrt{2}-1\right)}{3}\)

1: Gọi Q thuộc SD sao cho SQ/SD=1/3

=>PQ//DC

M,E lần lượt là trung điểm của SA,SB

=>ME//AB

=>PQ//ME

=>\(Q\in\left(MEP\right)\)

Xét mp(SDB) có

QE ko song song với DB

=>QE cắt DB tại I

=>\(I=DB\cap\left(MPE\right)\)

2:

Đặt SA/SM=a; SC/SP=c; SD/SQ=d; SB/SN=b

V MPQ/V ACD=SM/SA*SP/SC*SQ/SD

=>V MPQ=1/2*V ABCD*1/acd

Tương tự, ta có: \(V_{MPN}=\dfrac{1}{acb}\cdot\dfrac{1}{2}\cdot V_{ABCD}\)

\(V_{MBN}=\dfrac{1}{bda}\cdot\dfrac{1}{2}\cdot V_{ABCD}\)

\(V_{PQN}=\dfrac{1}{2}\cdot\dfrac{1}{bdc}\cdot V_{ABCD}\)

=>V MNPQ=V MPQ+V NPQ

=V MBN+V PQN

\(=\dfrac{1}{2}\cdot V_{ABCD}\left(\dfrac{1}{acd}+\dfrac{1}{acb}\right)\)

=>1/acd+1/acb=1/bda+1/bdc

=>b+d=a+c

=>SB/SN+SD/SQ=SA/SM+SC/SP=2+3=5

Bài có trên Web 

Tham khảo nhé!

https://hoc24.vn/cau-hoi/cho-hinh-chop-sabc-co-tam-giac-abc-vuong-tai-a-goc-abc60-sbaba-hai-mat-ben-sab-va-sbc-cung-vuong-goc-voi-mat-day-goi-hk-lan-luot-la.898787451803

\(AB\) // CD \(\Rightarrow\left(SAB\right)\cap\left(SCD\right)=Sx\) // AB // CD  

SA \(\perp\) đáy \(\Rightarrow SA\perp AB\) ; mà AB // Sx \(\Rightarrow SA\perp Sx\)

Dễ dàng c/m : \(CD\perp\left(SAD\right)\Rightarrow CD\perp SD\) ; mà Sx // CD . Suy ra : \(SD\perp Sx\)

Suy ra : \(\left(\left(SAB\right);\left(SCD\right)\right)=\left(SA;SD\right)=\widehat{ASD}\)

\(\Delta SAD\perp\) tại A có : \(tan\widehat{ASD}=\dfrac{AD}{AS}=\dfrac{a}{\sqrt{3}a}=\dfrac{1}{\sqrt{3}}\Rightarrow\widehat{ASD}=30^o\)

\(\Rightarrow\left(\left(SAB\right);\left(SCD\right)\right)=30^o\)