Bài 6: Ôn tập chương Vecơ trong không gian. Quan hệ vuông góc trong không gian.
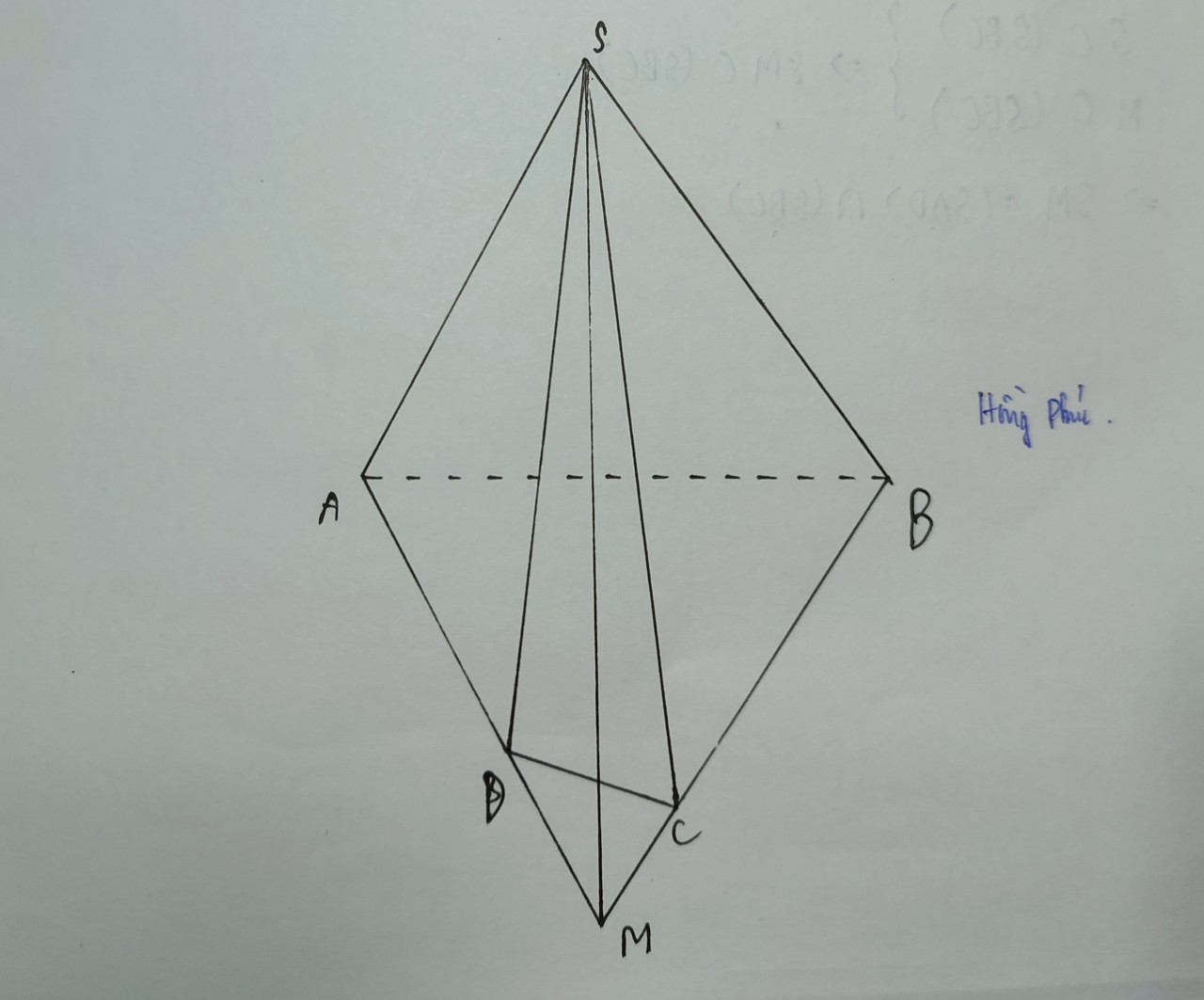
GIÚP EM VỚI,EM ĐANG CẦN GẤP Cho tứ diện ABCD gọi I,J là các điểm lần lượt nằm trên AB,AD với AI=1/2,AJ=3/2JD.Tìm giao tuyến của:
a)(ACD)∩(CIJ)
b)(CIJ)∩(BCD)
Giúp mình với ạ!
Đọc tiếp
Giúp mình với ạ!
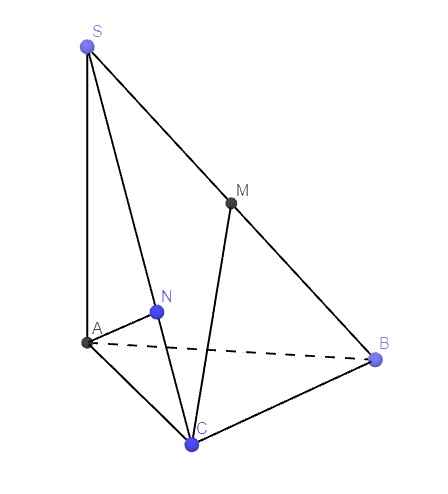
\(\overrightarrow{AN}=\overrightarrow{AS}+\overrightarrow{SN}=\overrightarrow{AS}+\dfrac{2}{3}\overrightarrow{SC}=\overrightarrow{AS}+\dfrac{2}{3}\overrightarrow{SA}+\dfrac{2}{3}\overrightarrow{AC}=\dfrac{1}{3}\overrightarrow{AS}+\dfrac{2}{3}\overrightarrow{AC}\)
\(\overrightarrow{CM}=\dfrac{1}{2}\overrightarrow{CS}+\dfrac{1}{2}\overrightarrow{CB}=\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{AS}+\dfrac{1}{2}\overrightarrow{CB}\)
\(AN\perp CM\Rightarrow\overrightarrow{AN}.\overrightarrow{CM}=0\)
\(\Rightarrow\left(\overrightarrow{AS}+2\overrightarrow{AC}\right)\left(\overrightarrow{CA}+\overrightarrow{AS}+\overrightarrow{CB}\right)=0\)
\(\Rightarrow\overrightarrow{AS}\left(\overrightarrow{CA}+\overrightarrow{CB}\right)+AS^2-2AC^2+2\overrightarrow{AC}.\overrightarrow{AS}-2\overrightarrow{CA}.\overrightarrow{CB}=0\)
\(\Leftrightarrow AS^2-2AC^2-2\overrightarrow{CA}.\overrightarrow{CB}=0\)
\(\Leftrightarrow x^2-2a^2-2a^2.cos60^0=0\)
\(\Leftrightarrow x^2-3a^2=0\)
\(\Leftrightarrow x=a\sqrt{3}\)
Vậy \(SA=a\sqrt{3}\) thì \(AN\perp CM\)
Đúng 1
Bình luận (0)
Cho hình chóp SABCD đáy ABCD là hình vuông cạch a SAB là tam giác đều và vuông góc (ABCD) .Gọi H là trung điểm AB a, Chứng minh SH vuông góc với (ABCD) b, chứng minh tam giác SBC vuông cân c, gọi I là trung điểm chứng minh SC vuông góc với DI
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, đáy lớn BC=2a, AB=AD=a, SB vuông góc (ABCD), SB= a√3 a. CM ∆SAD vuông b. CM DC vuông góc (SBD) c. Gọi O là giao điểm của AC và BD, (alpha) là mp qua O và vuông góc với AB. Tìm và tính thiết diện của hình chóp cắt bởi (alpha)
Giúp mình với mn ơi huhu
Giúp mik câu này vs đc ko mn
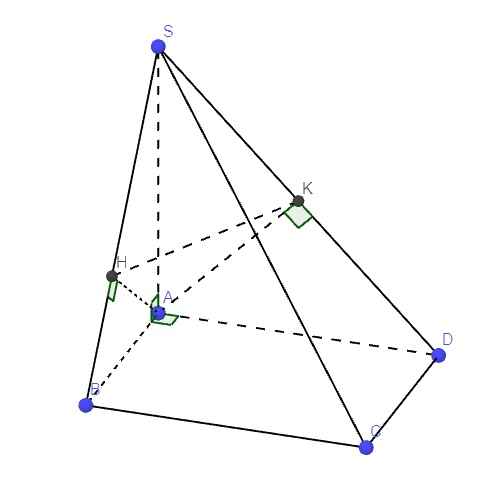
\(SA\perp\left(ABCD\right)\Rightarrow\left\{{}\begin{matrix}SA\perp AB\\SA\perp AD\end{matrix}\right.\) \(\Rightarrow\) các tam giác SAB và SAD vuông tại A
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\)
\(\Rightarrow\Delta SBC\) vuông tại B
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp SD\)
\(\Rightarrow\Delta SCD\) vuông tại D
b.
\(\left\{{}\begin{matrix}BC\perp\left(SAB\right)\Rightarrow BC\perp AH\\AH\perp SB\end{matrix}\right.\) \(\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp SC\) (1)
\(\left\{{}\begin{matrix}CD\perp\left(SAD\right)\Rightarrow CD\perp AK\\AK\perp SD\end{matrix}\right.\) \(\Rightarrow AK\perp\left(SCD\right)\Rightarrow AK\perp SC\) (2)
(1);(2) \(\Rightarrow SC\perp\left(AHK\right)\)
Đúng 1
Bình luận (0)
Giúp mình câu này với mình đang cần gấp
a: \(\widehat{\left(SC;\left(ABCD\right)\right)}=\widehat{CS;CA}=\widehat{SCA}\)
Ta có: SA\(\perp\)(ABCD)
=>SA\(\perp\)AC
=>ΔSAC vuông tại A
Vì ABCD là hình vuông
nên \(AC=AD\cdot\sqrt{2}=a\sqrt{2}\)
Xét ΔSAC vuông tại A có \(tanSCA=\dfrac{SA}{AC}=\dfrac{a\sqrt{6}}{a\sqrt{2}}=\sqrt{3}\)
nên \(\widehat{SCA}=60^0\)
=>\(\widehat{SC;\left(ABCD\right)}=60^0\)
b: Ta có: BD\(\perp\)AC
BD\(\perp\)SA
SA,AC cùng thuộc mp(SAC)
Do đó: BD\(\perp\)(SAC)
\(\widehat{SB;\left(SAC\right)}=\widehat{SB;SD}=\widehat{BSD}\)
Vì ABCD là hình vuông
nên \(AC=BD=a\sqrt{2}\)
ΔSAD vuông tại A
=>\(SA^2+AD^2=SD^2\)
=>\(SD^2=\left(a\sqrt{6}\right)^2+a^2=7a^2\)
=>\(SD=a\sqrt{7}\)
ΔSAB vuông tại A
=>\(SA^2+AB^2=SB^2\)
=>\(SB=a\sqrt{7}\)
Xét ΔSBD có \(cosBSD=\dfrac{SB^2+SD^2-BD^2}{2\cdot SB\cdot SD}\)
\(=\dfrac{7a^2+7a^2-2a^2}{2\cdot a\sqrt{7}\cdot a\sqrt{7}}=\dfrac{6}{7}\)
=>\(sinBSD=\sqrt{1-\left(\dfrac{6}{7}\right)^2}=\dfrac{\sqrt{13}}{7}\)
=>\(\widehat{BSD}\simeq31^0\)
=>\(\widehat{SB;\left(SAC\right)}\simeq31^0\)
Đúng 0
Bình luận (0)
Câu cuối ạ
Ủa sao cứ lỗi link nhỉ?
https://hoc24.vn/cau-hoi/giup-em-voi-em-cam-on-nhieu-a.5325836283216
Đúng 0
Bình luận (0)
Mọi người ơi giúp mình câu 3 với ạ🙏🙏🙏

3:
a: CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>(SBC) vuông góc (SAB)
Đúng 0
Bình luận (0)