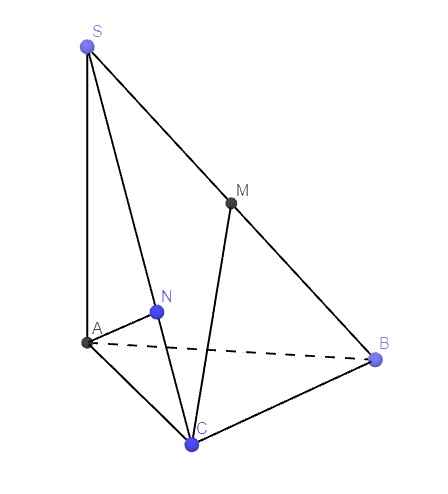
\(\overrightarrow{AN}=\overrightarrow{AS}+\overrightarrow{SN}=\overrightarrow{AS}+\dfrac{2}{3}\overrightarrow{SC}=\overrightarrow{AS}+\dfrac{2}{3}\overrightarrow{SA}+\dfrac{2}{3}\overrightarrow{AC}=\dfrac{1}{3}\overrightarrow{AS}+\dfrac{2}{3}\overrightarrow{AC}\)
\(\overrightarrow{CM}=\dfrac{1}{2}\overrightarrow{CS}+\dfrac{1}{2}\overrightarrow{CB}=\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{AS}+\dfrac{1}{2}\overrightarrow{CB}\)
\(AN\perp CM\Rightarrow\overrightarrow{AN}.\overrightarrow{CM}=0\)
\(\Rightarrow\left(\overrightarrow{AS}+2\overrightarrow{AC}\right)\left(\overrightarrow{CA}+\overrightarrow{AS}+\overrightarrow{CB}\right)=0\)
\(\Rightarrow\overrightarrow{AS}\left(\overrightarrow{CA}+\overrightarrow{CB}\right)+AS^2-2AC^2+2\overrightarrow{AC}.\overrightarrow{AS}-2\overrightarrow{CA}.\overrightarrow{CB}=0\)
\(\Leftrightarrow AS^2-2AC^2-2\overrightarrow{CA}.\overrightarrow{CB}=0\)
\(\Leftrightarrow x^2-2a^2-2a^2.cos60^0=0\)
\(\Leftrightarrow x^2-3a^2=0\)
\(\Leftrightarrow x=a\sqrt{3}\)
Vậy \(SA=a\sqrt{3}\) thì \(AN\perp CM\)