Cho tam giác ABC có AB = AC.Lấy điểm E trên AB,điểm F trên AC sao cho AE = AF.
a)Chứng minh BF = CE và tam giác BEC = tam giác CFB.
b)Biết BF cắt CE tại I.Cho biết IE = IF.Chứng minh tam giác IBE = tam giác ICF
Bài 4: Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
a: Xét ΔABF và ΔACE có
AB=AC
\(\widehat{BAF}\) chung
AF=AE
Do đó: ΔABF=ΔACE
=>BF=CE
AE+EB=AB
AF+FC=AC
mà AE=AF và AB=AC
nên EB=FC
Xét ΔEBC và ΔFCB có
EB=FC
BC chung
EC=FB
Do đó: ΔEBC=ΔFCB
b: ΔABF=ΔACE
=>\(\widehat{ABF}=\widehat{ACE}\)
=>\(\widehat{IBE}=\widehat{ICF}\)
ΔBEC=ΔCFB
=>\(\widehat{BEC}=\widehat{CFB}\)
=>\(\widehat{IEB}=\widehat{IFC}\)
Xét ΔIEB và ΔIFC có
\(\widehat{IEB}=\widehat{IFC}\)
BE=CF
\(\widehat{IBE}=\widehat{ICF}\)
Do đó: ΔIEB=ΔIFC
Đúng 1
Bình luận (0)
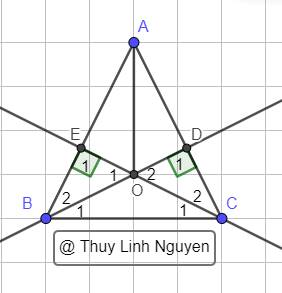
Cho tam giác ABC ( A < 90 độ), AB = AC.Kẻ CE vuông góc AB (E thuộc AB).Kẻ BD vuông góc AC,(D thuộc AC).Gọi O là giao điểm của BD và CE.
a)Chứng minh BD = CE
b)Chứng minh OE = OD và OB = OC
c)Chứng minh OA là phân giác BAC
Giúp mình nhé mình cần gấp
`a)`
Có `Delta ABC` cân tại `A(g t)`
`=>hat(ABC)=hat(ACB)`
`=>hat(EBC)=hat(DCB)`
Xét `Delta BEC` và `Delta CDB` có :
`{:(hat(E_1)=hat(D_1)(=90^0)),(BC-chung),(hat(EBC)=hat(DCB)(cmt)):}}`
`=>Delta BEC=Delta CDB(c.h-g.n)`
`=>CE=BD` ( 2 cạnh tương ứng )( dpcm )
`b)`
Có `Delta BEC=Delta CDB(cmt)`
`=>hat(C_1)=hat(B_1)` ( 2 góc tương ứng )
`=>Delta BOC` cân tại `O`
`=>OB=OC`(dpcm)
Xét `Delta OEB` và `Delta ODC` có :
`{:(hat(E_1)=hat(D_1)(=90^0)),(OB=OC(cmt)),(hat(O_1)=hat(O_2)(doi.di nh)):}}`
`=>Delta OEB=Delta ODC(c.h-g.n)`
`=>OE=OD`( 2 cạnh tương ứng )(dpcm)
`c)`
Có `Delta ABC` cân tại `A(g t)`
`=>AB=AC`
`=>A in ` trung trực của `Delta ABC(1)`
Có `OB=OC(cmt)`
`=>O in` trung trực của `Delta ABC(2)`
Từ `(1)` và `(2)=>OA` là trung trực `Delta ABC`
mà `Delta ABC` cân tại `A`
Nên `OA` là phân giác `hat(BAC)` (dpcm)
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A và M là trung điểm của BC.Gọi N là trung điểm của AB,trên tia đối của tia NC lấy điểm K sao cho NK = NC.
a)Chứng minh tam giác ABM = tam giác ACM
b)Chứng minh rằng AK = 2.MC
c)Tính số đo của MAK
Giúp em với ạ(nếu ko phiền thì kèm thêm hình vẽ ạ)
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Xét ΔNBC và ΔNAK có
NB=NA
\(\widehat{BNC}=\widehat{ANK}\)(hai góc đối đỉnh)
NC=NK
Do đó: ΔNBC=ΔNAK
=>BC=AK
mà BC=2MC
nên AK=2MC
c: ΔNBC=ΔNAK
=>\(\widehat{NBC}=\widehat{NAK}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BC//AK
ΔABC cân tại A
mà AM là đường trung tuyến
nên AM\(\perp\)BC
mà BC//AK
nên AM\(\perp\)AK
=>\(\widehat{KAM}=90^0\)
Đúng 1
Bình luận (0)
Bài 53: Cho tam giác ABC vuông tại A. Trên tia đối của tia AC lấy điểm D sao cho AD AC.b) Chứng minh: AABC AABD.b) Trên tia đối của tia AB lấy điểm M. Chứng minh: MD MCBài 55: Cho tam giác ABC có A 90°, tia phân giác BD của góc B (D ∈ AC). Trên cạnh BC lấy điểm E sao cho BE BA.a) So sánh độ dài các đoạn AD và DE, so sánh EDC và ABC.b) Chứng minh: AEBD.Bài 56: Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME MA.a) Chứng minh rằng: AC//BE.b) Gọi I là một...
Đọc tiếp
Bài 53: Cho tam giác ABC vuông tại A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC.
b) Chứng minh: AABC = AABD.
b) Trên tia đối của tia AB lấy điểm M. Chứng minh: MD = MC
Bài 55: Cho tam giác ABC có A =90°, tia phân giác BD của góc B (D ∈ AC). Trên cạnh BC lấy điểm E sao cho BE = BA.
a) So sánh độ dài các đoạn AD và DE, so sánh EDC và ABC.
b) Chứng minh: AEBD.
Bài 56: Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA.
a) Chứng minh rằng: AC//BE.
b) Gọi I là một điểm trên cạnh AC, K là một điểm trên cạnh EB sao cho AI = EK. Chứng minh ba điểm I, M,K thẳng hàng.
Bài 55:
a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
=>DA=DE
Ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}=90^0\)
=>DE\(\perp\)BC tại E
Ta có: \(\widehat{EDC}+\widehat{C}=90^0\)(ΔEDC vuông tại E)
\(\widehat{ABC}+\widehat{C}=90^0\)(ΔABC vuông tại A)
Do đó: \(\widehat{EDC}=\widehat{ABC}\)
b: ta có: ΔBAD=ΔBED
=>DA=DE
=>D nằm trên đường trung trực của AE(1)
Ta có:BA=BE
=>B nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
=>BD\(\perp\)AE
Bài 56:
a: Xét tứ giác ABEC có
M là trung điểm chung của AE và BC
=>ABEC là hình bình hành
=>AC//BE và AC=BE
b: Xét ΔIAM và ΔKEM có
IA=KE
\(\widehat{IAM}=\widehat{KEM}\)(hai góc so le trong, AC//BE)
MA=ME
Do đó: ΔIAM=ΔKEM
=>\(\widehat{IMA}=\widehat{KME}\)
mà \(\widehat{IMA}+\widehat{IME}=180^0\)(hai góc kề bù)
nên \(\widehat{KME}+\widehat{IME}=180^0\)
=>K,M,I thẳng hàng
Đúng 1
Bình luận (0)
Cho đoạn thẳng AB có M là M là trung điểm. Qua M kẻ đường thẳng d vuông góc với AB. Lấy cd (c \(\ne\)M). Chứng minh CM là tia phân giác của góc ACB
Xem chi tiết
Xét ΔCMA vuông tại M và ΔCMB vuông tại M có
CM chung
MA=MB
Do đó: ΔCMA=ΔCMB
=>\(\widehat{ACM}=\widehat{BCM}\)
=>CM là phân giác của góc ACB
Đúng 0
Bình luận (0)
Cho Tam giác ABC nhọn, M là trung điểm BC. Đường vuông góc AB tại B cắt AM tại D. Trên tia MD lấy E. ME=MD. EC cắt AB tại k.Cm: a. Tam giác EHC=Tam giác DMB
b. Tam giác AKI vuông tại k
giúp mình với cô mình giao bài như này nhưng mình thì ko hiểu đc luôn Á. Giúp mình với nha!!!!!
Cho tam giác BCD có BC = BD và tia phân giác của góc B cắt EC ở H
a) Chứng minh:tam giác BCD= BDH
b) Chứng minh: BH là tia phân giác của CD
a: Sửa đề: cắt CD tại H. Chứng minh ΔBCH=ΔBDH
Xét ΔBHC và ΔBHD có
BH chung
\(\widehat{HBC}=\widehat{HBD}\)(BH là phân giác của góc CBD)
BC=BD
Do đó: ΔBHC=ΔBHD
b: Bạn ghi lại đề nha bạn
Đúng 1
Bình luận (0)
Bài 1: Cho góc xOy nhọn có Oz là phân giác . Lấy A e tia Ox ; B e tia Oy sao cho OA = OB . Lấy C e tia Oz
a) C/m AC = CB
b) Gọi I là giao của AB với OC . C/m AB ⊥ Oc tại I
Bài 2: Cho góc xOy ∠ 90* . Trên tia Ox lấy A và C , trên tia Oy lấy B và D sao cho OA = OB ; OC = OD (A nằm giữa O và C )
a) Gọi I là giao của AD với BC . C/m Oy là phân giác của xOy
Bài 1:
a: Xét ΔOAC và ΔOBC có
OA=OB
góc AOC=góc BOC
OC chung
Do đo: ΔOAC=ΔOBC
Suy ra: CA=CB
b: Ta có: ΔOAB cân tại O
mà OI là đường phân giác
nên OI là đường cao
Đúng 1
Bình luận (0)
3 đoạn thẳng AA,BB,CCcắt nhau tại O là trung điểm của mỗi đoạn thẳng sao cho tam giác ABC và tam giác ABC ở hai phía khác nhau đối với một đường thẳng d đi qua điểm O. Chứng Minh:
a. tam giac OAB tam giác OAB
b. ACAC
c. tam giác ABCtam giác ABC
Mọi người giải chi tiết hộ em. Em cảm ơn!
d O A A C C B B
Đọc tiếp
3 đoạn thẳng AA',BB',CC'cắt nhau tại O là trung điểm của mỗi đoạn thẳng sao cho tam giác ABC và tam giác A'B'C' ở hai phía khác nhau đối với một đường thẳng d đi qua điểm O. Chứng Minh:
a. tam giac OAB = tam giác OA'B'
b. AC=A'C'
c. tam giác ABC=tam giác A'B'C
Mọi người giải chi tiết hộ em. Em cảm ơn!
a) Xét tam giác OAB và tam giác OA'B' có:
OB = OB' (gt)
∠BOA=∠B'OA' ( 2 góc đối đỉnh )
OA = OA' (gt)
=> tam giác OAB= tam giác OA'B' (c.g.c)
Đúng 0
Bình luận (2)
b) Xét tam giác OCA và tam giác OC'A' có :
OC=OC' (gt)
∠COA=∠C'OA' ( 2 góc đối đỉnh )
OA=OA' (gt)
=> tam giác OCA=tam giác OC'A' (c.g.c)
=> AC=A'C'
Đúng 0
Bình luận (0)
c) Ta có : ∠BAC + ∠BAO = ∠CAO
∠B'A'C' + ∠B'A'O = ∠C'A'O
Mà ∠BAO=∠B'A'O ( tam giác OAB= tam giác OA'B' )
∠CAO=∠C'A'O ( tam giác OAC = tam giác OA'C' )
=> ∠BAC=∠B'A'C'
Xét tam giác ABC và tam giác A'B'C' có :
AB=A'B' ( tam giác OAB = tam giác OA'B' )
AC=A'C' ( tam giác OAC = tam giác OA'C' )
∠BAC = ∠B'A'C' ( chứng minh trên )
=> tam giác ABC=tam giác A'B'C' (c.g.c)
Đúng 0
Bình luận (0)
Cho \(\Delta\)ABC có 3 góc nhọn ( AB < AC ). Vẽ tia phân giác AD ( D \(\in\) BC ). Trên AC, lấy điểm E sao cho AE = AB. Nối D và E.
a) Chứng minh: DB = DE
b) Tia ED cắt AB tại H. Chứng minh: \(\Delta\)DBH = \(\Delta\)DEC
c) Chứng minh: DHB = DCE
d) Chứng minh: AH = AC
a: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
Do đo: ΔABD=ΔAED
Suy ra: DB=DE
b: Xét ΔDBH và ΔDEC có
góc DBH=góc DEC
DB=DE
góc BDH=góc EDC
Do đó: ΔDBH=ΔDEC
c: Ta có: ΔDBH=ΔDEC
nên góc DHB=góc DCE
d: Ta có: AH=AB+BH
AC=AE+EC
mà AB=AE; BH=EC
nên AH=AC
Đúng 0
Bình luận (0)















