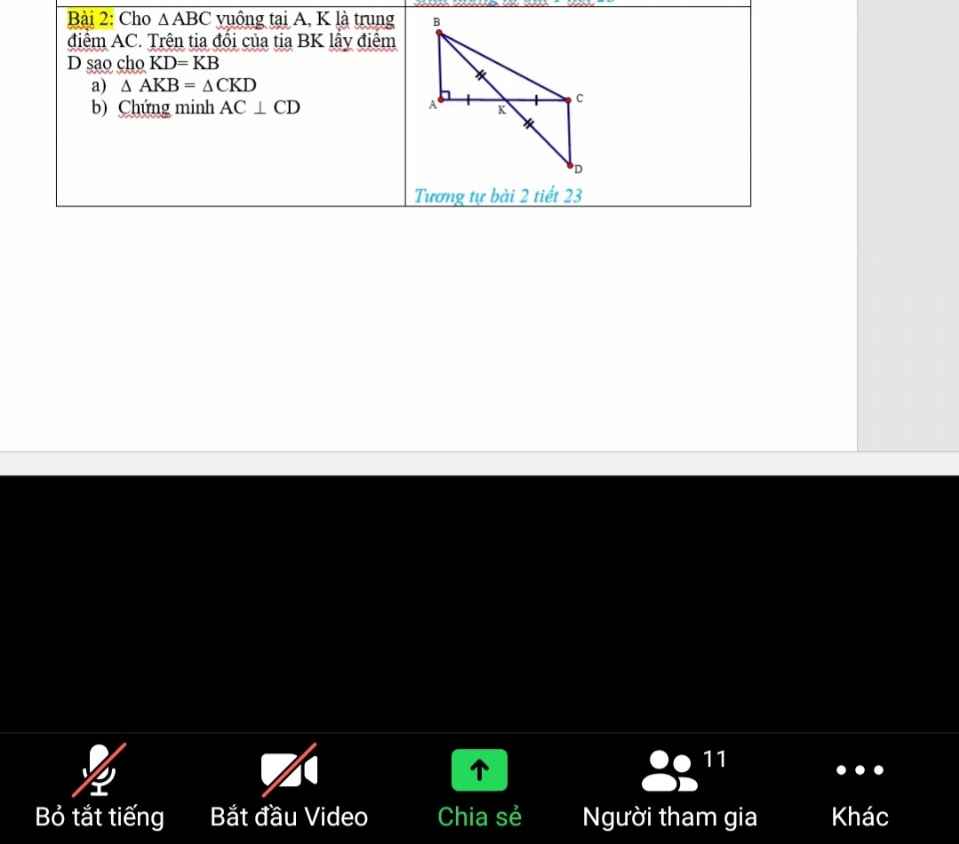
Bài 4: Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
a) Xét ΔAKB và ΔCKD
BK=KD (gt)
AK=CK (gt)
\(\widehat{BKA}=\widehat{CKD}\) (đối đỉnh)
⇒ ΔAKB = ΔCKD (c.g.c)
b) Vì ΔAKB = ΔCKD
⇒ \(\widehat{A}=\widehat{ACD}=90^0\) (hai góc tương ứng)
⇒ AC ⊥ CD
Đúng 2
Bình luận (0)
Bài 1: Cho tam giác ABC. Gọi I là trung điểm của AC. Trên tia đối của tia IB lấy điểm E sao cho IE = IB. Chứng minh rằng :
a) AE = BC; b)AB // EC
Bài 2: Cho góc xOy.Trên cạnh Ox lấy các điểm A và B, trên cạnh Oy lấy các điểm C và D sao cho OA = OC, OB = OD. Chứng minh rằng: AD = BC
Bài 1:
a: Xét tứ giác ABCE có
I là trung điểm của AC
I là trung điểm của BE
Do đó: ABCE là hình bình hành
Suy ra: AE=BC
b: Ta có: ABCE là hình bình hành
nên AB//EC
Đúng 0
Bình luận (0)
cho tam giác ABC có A<90. Trên nửa mp ko chứa đỉnh C có bờ là đường thẳng AB ta kẻ tia AE vuông góc AB và AE= AB . Trên nửa mp ko chứa đỉnh B bờ là đường thẳng AC ta kẻ tia AD vuông góc AC và AB=AC .Nối E với D. Gọi M và N lần lượt là trung điểm của các cạnh BC và ED .CM a) tam giác ABC=tam giác ADE
Hình như đề sai hay sao ấy. Bạn xem lại thử
Đúng 0
Bình luận (0)
Cho đoạn thẳng AB có M là M là trung điểm. Qua M kẻ đường thẳng d vuông góc với AB. Lấy cd (c \(\ne\)M). Chứng minh CM là tia phân giác của góc ACB
Xem chi tiết
Xét ΔCMA vuông tại M và ΔCMB vuông tại M có
CM chung
MA=MB
Do đó: ΔCMA=ΔCMB
=>\(\widehat{ACM}=\widehat{BCM}\)
=>CM là phân giác của góc ACB
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = AC.Lấy điểm E trên AB,điểm F trên AC sao cho AE = AF.
a)Chứng minh BF = CE và tam giác BEC = tam giác CFB.
b)Biết BF cắt CE tại I.Cho biết IE = IF.Chứng minh tam giác IBE = tam giác ICF
a: Xét ΔABF và ΔACE có
AB=AC
\(\widehat{BAF}\) chung
AF=AE
Do đó: ΔABF=ΔACE
=>BF=CE
AE+EB=AB
AF+FC=AC
mà AE=AF và AB=AC
nên EB=FC
Xét ΔEBC và ΔFCB có
EB=FC
BC chung
EC=FB
Do đó: ΔEBC=ΔFCB
b: ΔABF=ΔACE
=>\(\widehat{ABF}=\widehat{ACE}\)
=>\(\widehat{IBE}=\widehat{ICF}\)
ΔBEC=ΔCFB
=>\(\widehat{BEC}=\widehat{CFB}\)
=>\(\widehat{IEB}=\widehat{IFC}\)
Xét ΔIEB và ΔIFC có
\(\widehat{IEB}=\widehat{IFC}\)
BE=CF
\(\widehat{IBE}=\widehat{ICF}\)
Do đó: ΔIEB=ΔIFC
Đúng 1
Bình luận (0)
Tam giác ABC vuông tại A . Phân giác B cắt AC tại D . Trên BC lấy M sao cho BA = BM
a) Chứng minh MD vuông góc BC
b) Chứng minh AM vuông góc BD
c)AMD = 36 độ
Tính B , C tam giác ABC
a: Xét ΔBAD và ΔBMD có
BA=BM
góc ABD=góc MBD
BD chung
=>ΔBAD=ΔBMD
=>góc BMD=90 độ
=>DM vuông góc BC
b: BA=BM
DA=DM
=>BD là trung trực của AM
=>BD vuông góc AM
c: góc AMD=36 độ
=>góc ADM=180-2*36=108 độ
=>góc ABC=72 độ
=>góc C=18 độ
Đúng 0
Bình luận (0)
chứng minh bc bằng mc
Cho tam giác ABC có D là trung điểm của AC. Trên tia đối của tia DB lấy điểm E sao
cho DB = DE. Chứng minh BC k AE.
Xét tứ giác ABCE có
D là trung điểm của AC
D là trung điểm của BE
Do đó: ABCE là hình bình hành
Suy ra: BC//AE
Đúng 0
Bình luận (0)
cho widehat{xOy} lấy A,C in Ox sao cho OCOA. Trên tia Oy lấy B và D sao cho OBOA,ODAC a, c/m:ADBC và Delta ABCDelta BAD b,Gọi I là giao điểm của AD và BC cho biết IAIB . Chứng minh OI là tia pg góc xOy
Đọc tiếp
cho \(\widehat{xOy}\) lấy A,C \(\in\) Ox sao cho OC<OA. Trên tia Oy lấy B và D sao cho OB=OA,OD=AC a, c/m:AD=BC và \(\Delta ABC=\Delta BAD\) b,Gọi I là giao điểm của AD và BC cho biết IA=IB . Chứng minh OI là tia pg góc xOy





















