a) Xét ΔAKB và ΔCKD
BK=KD (gt)
AK=CK (gt)
\(\widehat{BKA}=\widehat{CKD}\) (đối đỉnh)
⇒ ΔAKB = ΔCKD (c.g.c)
b) Vì ΔAKB = ΔCKD
⇒ \(\widehat{A}=\widehat{ACD}=90^0\) (hai góc tương ứng)
⇒ AC ⊥ CD
Gấp ạ!!!
CHO DEF VUÔNG TẠI D . TRÊN CẠNH EF LẤY K SAO CHO EK=ED . TIA PHÂN GIÁC CỦA GÓC E CẮT DF TẠI H
a) CHỨNG MINH DH=HK
b) TÍNH GÓC EKH
Giúp vs ạ!!! Gấp ạ
Vẽ hình nữa mới đc tick nha
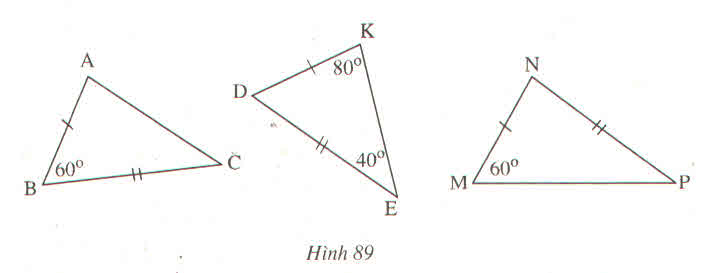
Trên hình 89 có các tam giác nào bằng nhau ?
cho AB//CD và AB=CD . chứng minh rằng
a, tam giác DAC = tam giác BCA
b , AD=BC
c, AD//BC
đ, gọi I là trung điểm của AC . K là trung điểm của AD . H là trung điểm của BC . Chứng minh IK=IH
e, chứng minh I là trung điểm của đoạn thẳng BD
cho tam giác ABC có AC > AB , phân giác AD của góc A . Lấy điểm E ∈ AC sao cho AE = AB . Chứng minh rằng
a, BD = DE
b, AD ⊥ với EB
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC ( H thuộc BC). Các tam giác AHC và BAC có AC là cạnh chung, góc C là góc chung, góc AHC = góc BAC = 90 độ, nhưng hai tam giác đó không bằng nhau. Tại sao ở đây không thể áp dụng trường hợp góc - cạnh - góc để kết luận \(\Delta\)AHC = \(\Delta\)BAC ?
tren canh ax va ay cua goc xay ,lan luot lay b va c sao cho ab=ac.ve tia az vuong goc voi ay va cat ã o e .so sanh tam giac abh va afc
Cho tam giác DEF vuông tại D, gọi M là trung điểm của EF. Trên tia đối của tia MD lấy điểm N sao cho MN = MD. Chứng minh NE // DF và NF // DE
