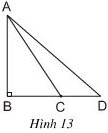
Cho tam giác ABC có M là trung điểm BC. Trên tia đối của tia MA lấy D, cho biết DB>DC. Hãy so sánh góc ABC và góc ACB
Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
Tam giác ABC vuông cân tại A. Trên nửa mặt phẳng bờ BC chứa A, vẽ tam giác BCD vuông tại D. Biết C, D cùng phía so với AB. Dx là tia đối của DC. CMR: AD là tia phân giác BDx.
tìm một cách chứng minh khác dinnh lý ở phần c trang 93
Cho tam giác ABC có AB khác AC. Lấy điểm M sao cho M nằm giữa B và C. Gọi E, F lần lượt là hình chiếu của B và C xuống AM. So sánh BE+CF với BC.
Trên cạnh BC của tam giác ABC cân tại A, lấy hai điểm D và E sao cho BD = DE = EC. CMR: góc BAD = EAC < DAE.
Xét ΔADB và ΔAEC có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đo: ΔADB=ΔAEC
Suy ra: \(\widehat{BAD}=\widehat{CAE}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC, 90* < B < 135*, C < 45*. Vẽ AD _|_ BC. CMR: BD < AD < CD.
Cho tam giác ABC. Gọi M là trung điểm của cạnh BC. Trên cạnh AB lấy điểm D. Tia DM cắt AC tại E. CMR MD < ME.
A K D O E F G B C P Q H
Đề : Cho (O), K là 1 điểm nằm ngoài đường tròn . KA;KD là các tiếp tuyến , KBC là 1 cát tuyến bất kì .Gọi E;F;G lần lượt là hình chiếu của D trên AB;AC;BC .Chứng minh rằng G là trung điểm EF.
Giải:
Trước tiên chứng minh E;F;G thẳng hàng .Đây chính là đường thẳng simson .
(*)Chứng minh G là trung điểm EF: Chứng minh trực tiếp trên hình vẽ có vẻ rất khó khăn nên tìm cách hạ đường vuông góc từ E;F xuống BC; sau đó chứng minh các khoảng cách bằng nhau.Từ đây ta lại...
Đọc tiếp
Đề : Cho (O), K là 1 điểm nằm ngoài đường tròn . KA;KD là các tiếp tuyến , KBC là 1 cát tuyến bất kì .Gọi E;F;G lần lượt là hình chiếu của D trên AB;AC;BC .Chứng minh rằng G là trung điểm EF.
Giải:
Trước tiên chứng minh E;F;G thẳng hàng .Đây chính là đường thẳng simson .
(*)Chứng minh G là trung điểm EF: Chứng minh trực tiếp trên hình vẽ có vẻ rất khó khăn nên tìm cách hạ đường vuông góc từ E;F xuống BC; sau đó chứng minh các khoảng cách bằng nhau.Từ đây ta lại nghĩ đến định lý thales nên hạ đường cao từ A xuống BC.
Kẻ EP; FQ; AH vuông góc với BC ( P;Q;H thuộc BC) \(\Rightarrow EP//AH//FQ\)
Theo định lý thales thì : \(\dfrac{EP}{AH}=\dfrac{EB}{AB}\); \(\dfrac{FQ}{AH}=\dfrac{FC}{AC}\) .Việc còn lại là chứng minh \(\dfrac{EB}{AB}=\dfrac{FC}{AC}\)hay \(\dfrac{EB}{FC}=\dfrac{AB}{AC}\)
Dễ dàng chứng minh:\(\Delta DBE\)~\(\Delta DCF\)(g.g) \(\Rightarrow\dfrac{EB}{FC}=\dfrac{DB}{DC}\)
Và \(\dfrac{BD}{DC}=\dfrac{KP}{KD}=\dfrac{KP}{KA}=\dfrac{AB}{AC}\) .Suy ra đpcm.
Do đó EP=FQ nên G là trung điểm EF
P/s: E Mượn chỗ gõ
Bài 1: Cho tam giác nhọn ABC, ABAC. Kẻ AH vuông góc với BC( H∈BC).Gọi M là một điểm nằm giữa A và H, tia BM cắt AC ở D. CMR
a)BMCM
b)DMDH
Bài 2: Cho tam giác Abc vuông ở A có ABac, phân giác AD. CMR
a)ADBADC
b)BDDC
Bài 3:Cho tam giác ABC vuông ở A, M là trung điểm AC. Gọi D và E lần lượt là hình chiếu của A và c xuống đường thẳng BM. So sánh tổng BD+BE với AB
Bài 4:CMR
a) trong một tam giác vuông cạnh đối diện với góc 300 bằng một nửa ca...
Đọc tiếp
Bài 1: Cho tam giác nhọn ABC, AB<AC. Kẻ AH vuông góc với BC( H∈BC).Gọi M là một điểm nằm giữa A và H, tia BM cắt AC ở D. CMR
a)BM<CM
b)DM<DH
Bài 2: Cho tam giác Abc vuông ở A có AB<ac, phân giác AD. CMR
a)ADB>ADC
b)BD>DC
Bài 3:Cho tam giác ABC vuông ở A, M là trung điểm AC. Gọi D và E lần lượt là hình chiếu của A và c xuống đường thẳng BM. So sánh tổng BD+BE với AB
Bài 4:CMR
a) trong một tam giác vuông cạnh đối diện với góc 300 bằng một nửa cạnh huyền
b) Trong một tam giác vuông có một cạnh góc vuông bằng một nửa cạnh huyền thì góc đối diện với cạnh ấy bẳng 300
P/s:mn giải đc bài nào giúp e vs ạ, e cần gấp
Bài 2:
a: AB<AC
nên \(\widehat{B}>\widehat{C}\)
Ta có: \(\widehat{BAD}+\widehat{B}+\widehat{ADB}=\widehat{CAD}+\widehat{C}+\widehat{ADC}\)
mà \(\widehat{BAD}=\widehat{CAD}\)
và \(\widehat{B}>\widehat{C}\)
nên \(\widehat{ADB}< \widehat{ADC}\)
b: Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
mà AB<AC
nên BD<CD
Đúng 0
Bình luận (0)
Cho tam giác ABCcó AB<AC. M là trung điểm của BC
Chứn minh: a, MAB>MAC
b, từ M kẻ Mx sao cho MA là tia phân giác của tia BMx ,Mx cắt BC ở D.Chứng minh :MB>MD
Vẽ hình cho mk luôn ạ
nhanh lên mk cần gấp