Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
Nội dung lý thuyết
1. Khái niệm đường vuông góc, đường xiên, hình chiếu của đường xiên
Từ điểm \(A\) không nằm trên đường thẳng \(d\), kẻ một đường thẳng vuông góc với \(d\) tại \(H\). Trên đường thẳng \(d\) lấy một điểm \(B\) không trùng với điểm \(H\) (hình vẽ). Khi đó:
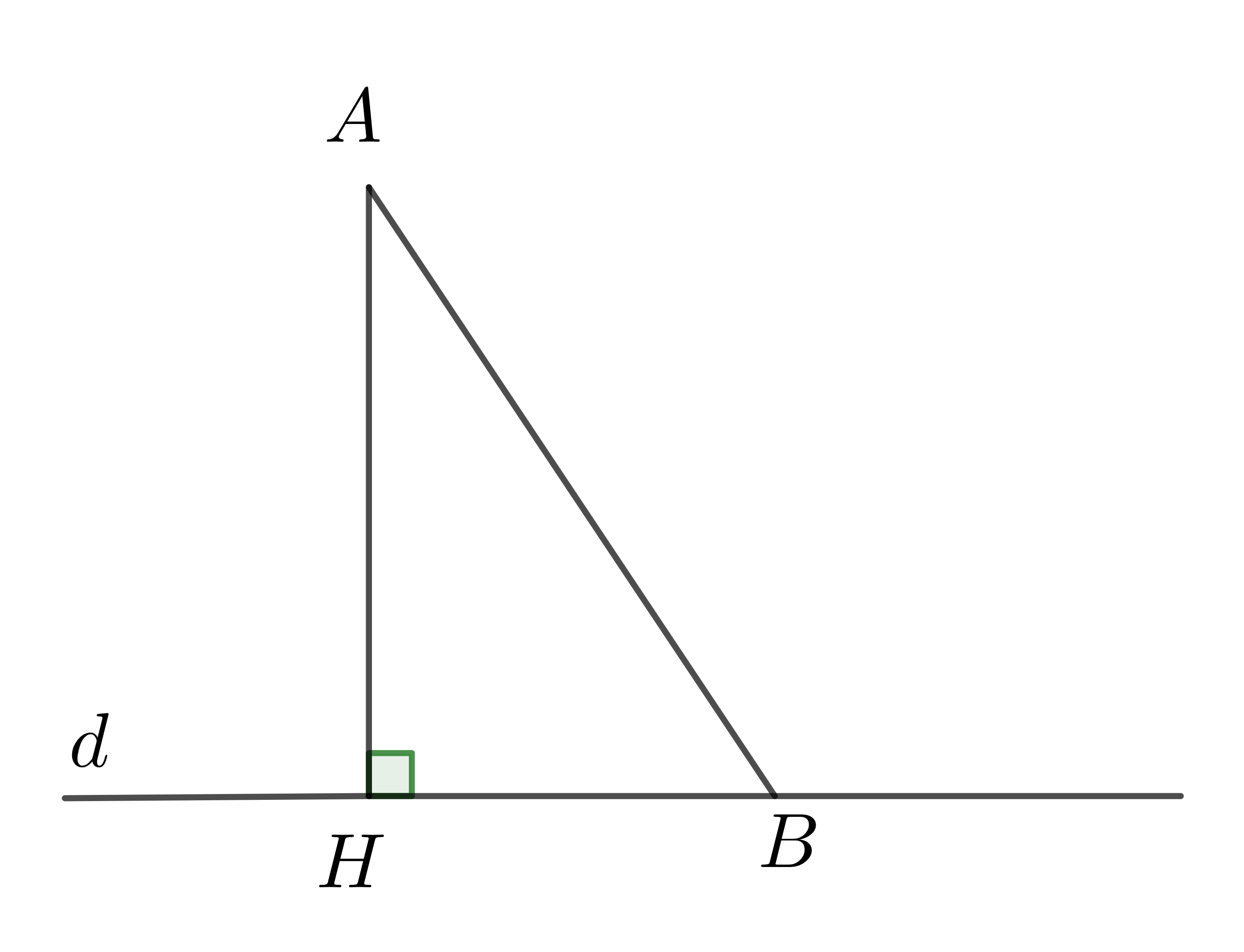
+) Đoạn thẳng \(AH\) gọi là đoạn vuông góc hay đường vuông góc kẻ từ điểm \(A\) đến đường thẳng \(d\), điểm \(H\) được gọi là chân của đường vuông góc hay hình chiếu của điểm \(A\) trên đường thẳng \(d\).
+) Đoạn thẳng \(AB\) gọi là một đường xiên kẻ từ điểm \(A\) đến đường thẳng \(d\).
+) Đoạn thẳng \(HB\) gọi là hình chiếu của đường xiên \(AB\) trên đường thẳng \(d\).
Ví dụ: Trong hình vẽ dưới đây:
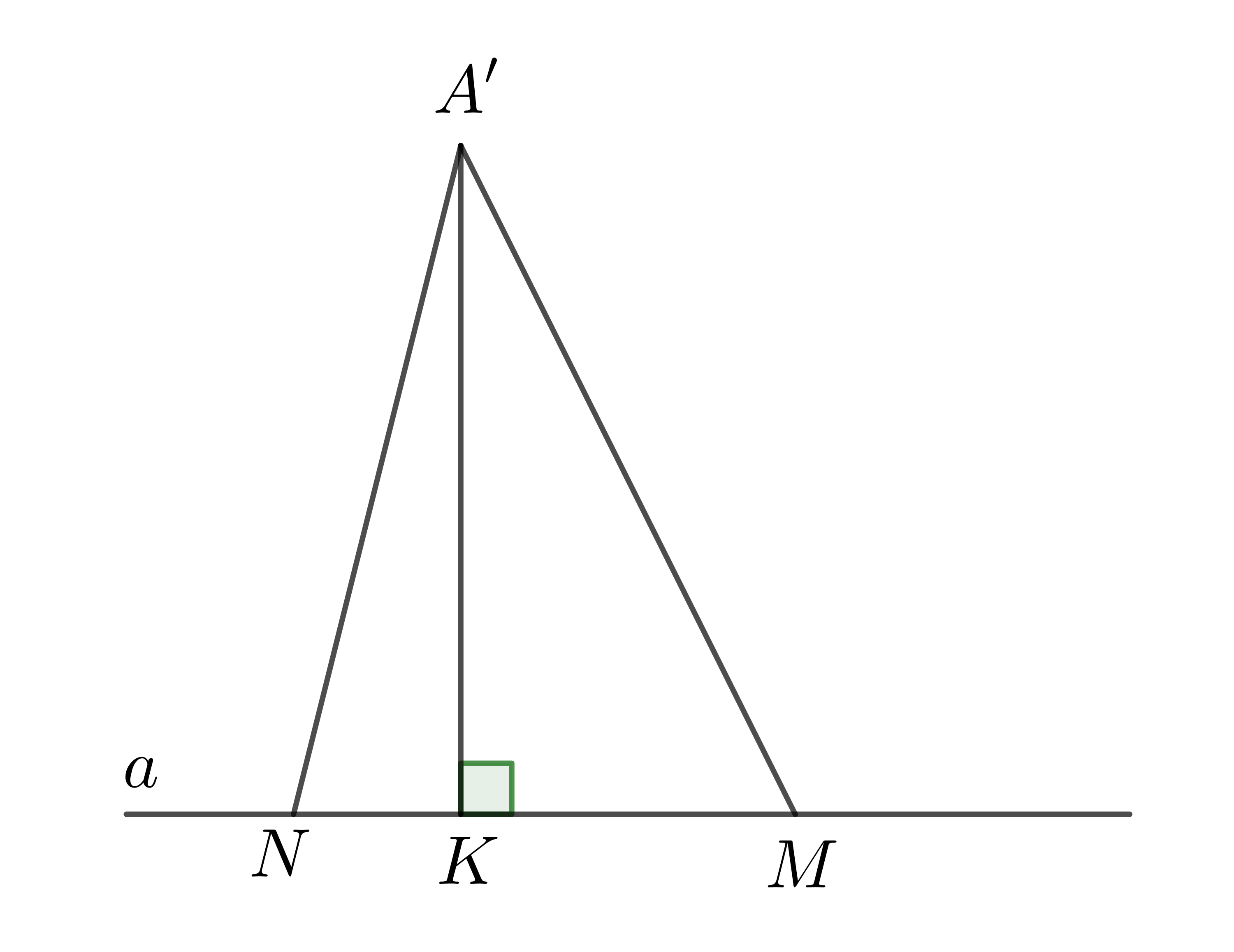
+) Đoạn thẳng \(A'K\) là đường vuông góc kẻ từ điểm \(A'\) đến đường thẳng \(a\). Điểm \(K\) gọi là chân đường vuông góchay hình chiếu của \(A'\) trên đường thẳng \(a\).
+) Đoạn thẳng \(A'M\) là một đường xiên kẻ từ \(A'\) đến đường thẳng \(a\). Đoạn thẳng \(KM\) là hình chiếu của đường xiên \(A'M\) trên đường thẳng \(a\).
+) Đoạn thẳng \(A'N\) là một đường xiên kẻ từ \(A'\) đến đường thẳng \(a\). Đoạn thẳng \(KN\) là hình chiếu của đường xiên \(A'N\) trên đường thẳng \(a\).
2. Quan hệ giữa đường vuông góc và đường xiên
Định lí 1:
Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
Cụ thể: Từ một điểm \(A\) nằm ngoài đường thẳng \(d\), kẻ đường vuông góc \(AH\) và một đường xiên \(AB\) tùy ý đến đường thẳng \(d\) thì \(AH< AB\).
| GT | \(A\notin d\) \(AH\) là đường vuông góc \(AB\) là đường xiên |
| KL | \(AH< AB\) |

Chứng minh:
Xét tam giác \(AHB\) vuông tại \(H\). Do \(AB\) là cạnh huyền, \(AH\) là cạnh góc vuông. Theo nhận xét về cạnh lớn nhất trong tam giác vuông, ta có \(AH< AB\).
Chú ý: Độ dài đường vuông góc \(AH\) gọi là khoảng cách từ điểm \(A\) đến đường thẳng \(d\).
@56069@
3. Các đường xiên và hình chiếu của chúng
Định lí 2:
Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó:
- Đường xiên nào có hình chiếu lớn hơn thì lớn hơn;
- Đường xiên nào lớn hơn thì có hình chiếu lớn hơn;
- Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau, và ngược lại, nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.
Ví dụ 1: Cho điểm \(A'\) nằm ngoài đường thẳng \(a\). Kẻ đường vuông góc \(A'K\) và các đường xiên \(A'M\), \(A'N\). Biết rằng \(KN=3cm\), \(KM=5,7cm\). So sánh \(A'K\), \(A'M\), \(A'N\)?
Giải:

Ta có: \(KN=3cm\), \(KM=5,7cm\) \(\Rightarrow KN< KM\)
Mà \(KN\), \(KM\) lần lượt là hình chiếu của \(A'N\), \(A'M\)
Theo định lí 2 ta suy ra \(A'N< A'M\)
Theo định lí 1 ta có \(A'K\) là đường nhỏ nhất
Do đó \(A'K< A'N< A'M\).
Ví dụ 2: Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Biết \(AB=2cm;AC=5cm\). So sánh \(HB\) và \(HC\)?
Giải:

Xét đường thẳng \(BC\) và điểm \(A\) nằm ngoài đường thẳng \(BC\)
Khi đó ta có đường vuông góc \(AH\), các đường xiên \(AB,AC\).
Nên \(HB\), \(HC\) lần lượt là hình chiếu của đường xiên \(AB,AC\) trên đường thẳng \(BC\)
Ta có: \(AB=2cm;AC=5cm\) \(\Rightarrow AB< AC\)
Theo định lí 2 ta suy ra \(HB< HC\).
Ví dụ 3: Cho tam giác \(ABC\) vuông tại \(A\). \(M\) là trung điểm \(AC\). Gọi \(D,E\) lần lượt là hình chiếu của \(A\) và \(C\) xuống đường thẳng \(BM\). So sánh \(\left(AD+CE\right)\) và \(2AB\)?
Giải:
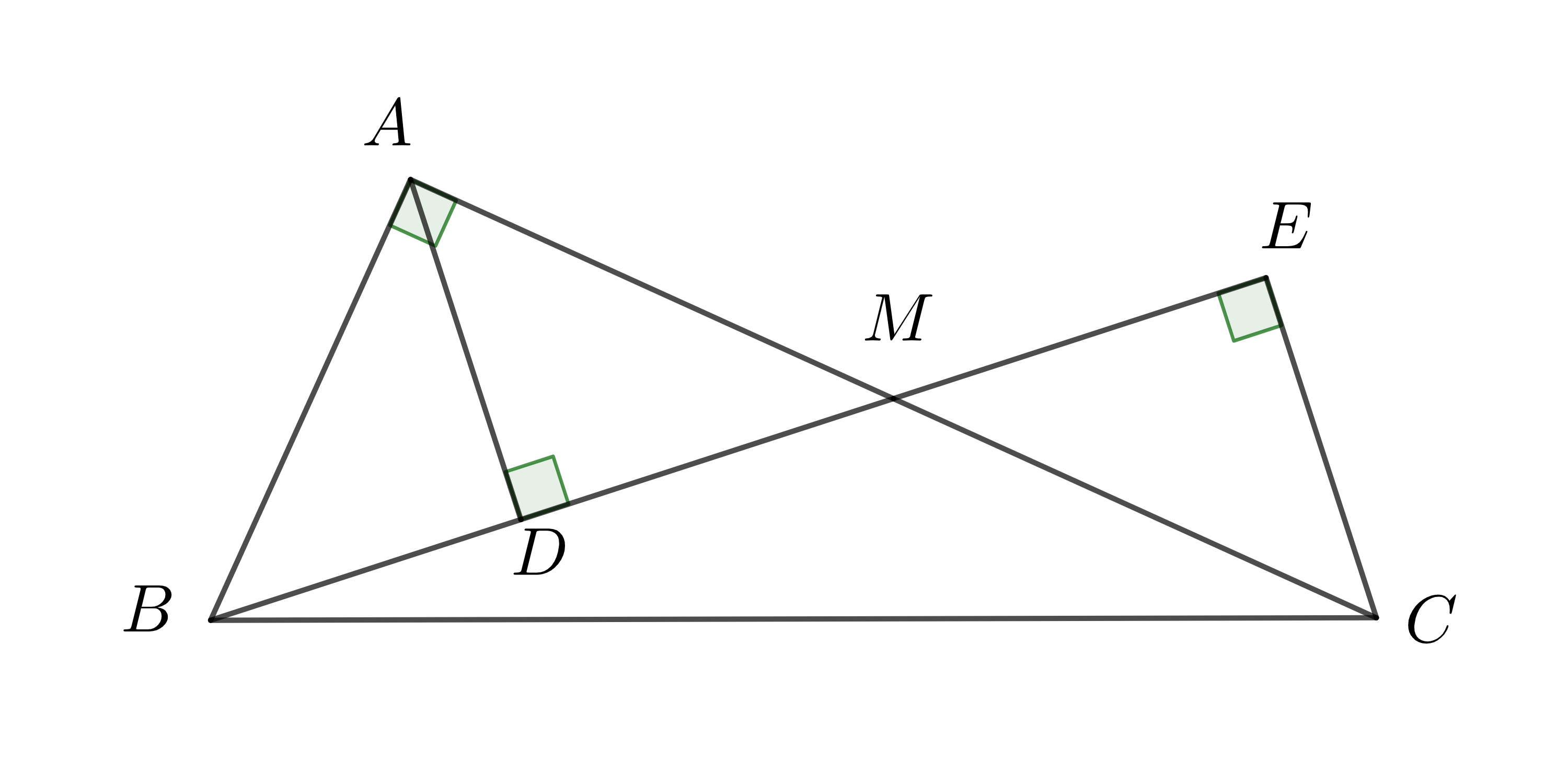
Do \(M\) là trung điểm \(AC\) nên \(MA=MC\)
Xét \(\Delta ADM\) và \(\Delta CEM\) vuông có:
\(MA=MC\)
\(\widehat{AMD}=\widehat{CME}\) (đối đỉnh)
\(\Rightarrow\Delta ADM=\Delta CEM\) (cạnh huyền - góc nhọn)
\(\Rightarrow AD=CE\) (hai cạnh tương ứng)
\(\Rightarrow AD+CE=2AD\)
Mặt khác ta có: \(AD< AB\) (quan hệ giữa đường vuông góc và đường xiên)
\(\Rightarrow2AD< 2AB\)
Hay \(AD+CE< 2AB\)
@56078@