Bài 1: Quan hệ giữa góc và cạnh đối diện trong một tam giác

1. Góc đối diện với cạnh lớn hơn

Định lí 1:

Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.

Chứng minh:

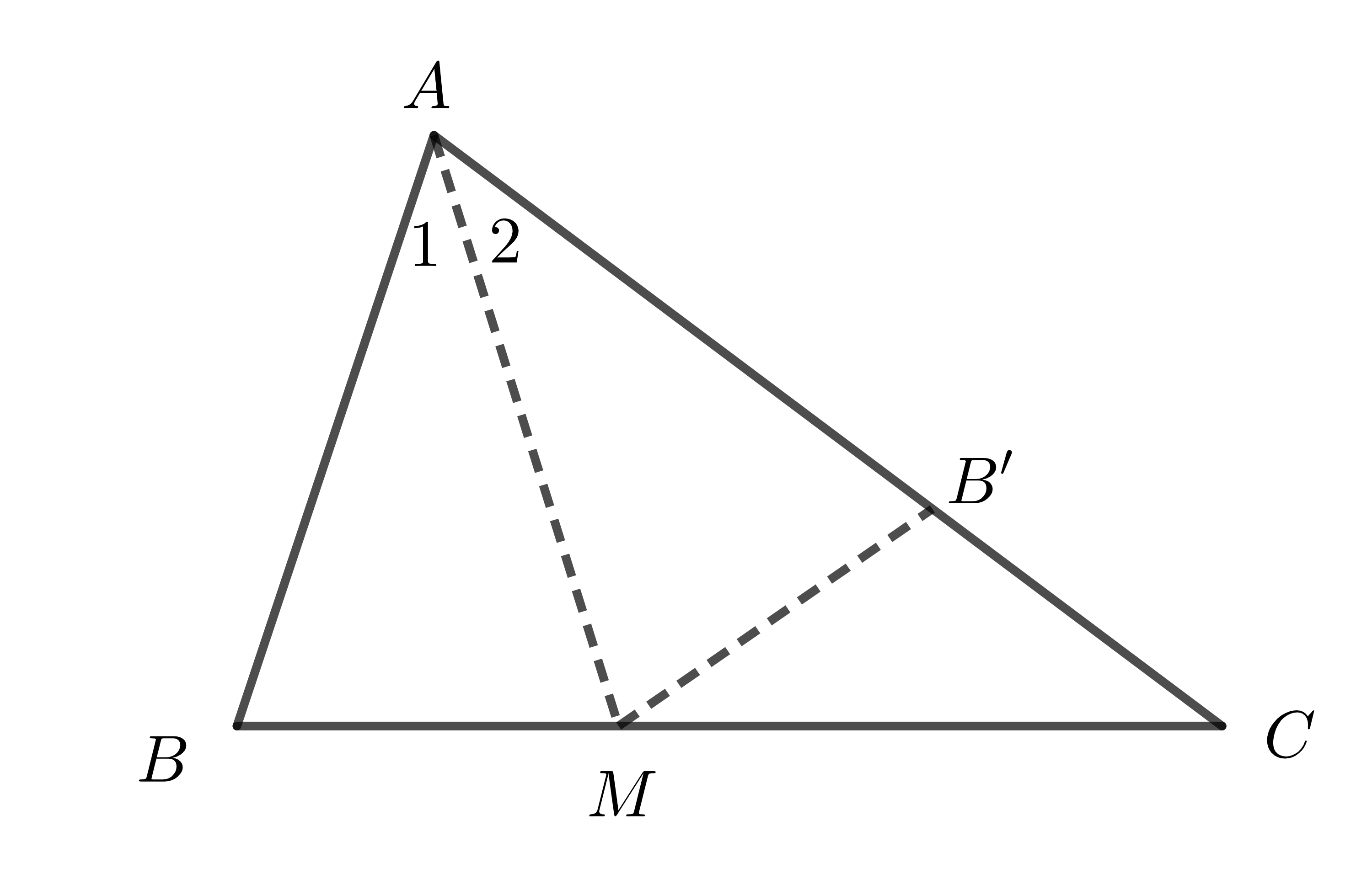
Trên tia \(AC\) lấy điểm \(B'\)sao cho \(AB=AB'\). Do \(AC>AB\) nên \(B'\) nằm giữa \(A\) và \(C\)

Kẻ tia phân giác \(AM\) của góc \(A\) (\(M\in BC\))

Xét \(\Delta ABM\) và \(\Delta AB'M\) có:

       \(AB=AB'\) (do cách lấy điểm \(B'\))

       \(\widehat{A_1}=\widehat{A_2}\) (do \(AM\) là tia phân giác góc \(A\))

       \(AM\) chung

\(\Rightarrow\Delta ABM=\Delta AB'M\) (c.g.c)

Suy ra \(\widehat{B}=\widehat{AB'M}\)     (1)

Lại có: \(\widehat{AB'M}\) là góc ngoài đỉnh \(B'\) của tam giác \(B'CM\) 

Theo tính chất phân giác ngoài ta có \(\widehat{AB'M}>\widehat{C}\)      (2)

Từ (1) và (2) suy ra \(\widehat{B}>\widehat{C}\).

Ví dụ 1: Cho tam giác \(ABC\) có \(AB=5cm\), \(AC=7cm\). So sánh góc \(\widehat{B}\) và \(\widehat{C}\) của tam giác \(ABC\).

Giải:

Ta nhận thấy \(\Delta ABC\) có \(AB< AC\) 

Theo định lí 1 ta suy ra \(\widehat{C}< \widehat{B}\)

Ví dụ 2: Cho tam giác \(DEF\) có độ dài các cạnh là \(DE=5cm\), \(EF=7cm\), \(DF=10cm\). So sánh các góc của tam giác \(DEF\).

Giải:

Ta nhận thấy \(\Delta DEF\) có \(DE< EF< DF\)

Nên theo định lí trên ta suy ra \(\widehat{F}>\widehat{D}>\widehat{E}\)

Ví dụ 3: Cho tam giác \(ABC\) có \(AB=4cm,AC=3cm,BC=6cm\). Gọi \(\widehat{A'},\widehat{B'},\widehat{C'}\) lần lượt là các góc ngoài đỉnh \(A,B,C\) của tam giác \(ABC\). So sánh các góc \(\widehat{A'},\widehat{B'},\widehat{C'}\).

Giải:

Ta nhận thấy \(\Delta ABC\) có \(AC< AB< BC\)

Theo định lí 1 ta suy ra \(\widehat{B}< \widehat{C}< \widehat{A}\)

\(\Rightarrow\) \(180^0-\widehat{B}>180^0-\widehat{C}>180^0-\widehat{A}\)

Do \(\widehat{A'},\widehat{B'},\widehat{C'}\) là các góc ngoài đỉnh \(A,B,C\) của \(\Delta ABC\)

Nên theo tính chất góc ngoài ta có \(\left\{{}\begin{matrix}\widehat{A'}=180^0-\widehat{A}\\\widehat{B'}=180^0-\widehat{B}\\\widehat{C'}=180^0-\widehat{C}\end{matrix}\right.\)

Suy ra \(\widehat{B'}>\widehat{C'}>\widehat{A'}\).

Ví dụ 4: Cho tam giác \(MNP\) có \(MN+PN=15cm\) ; \(MN-PN=5cm\). So sánh góc \(M\) và góc \(P\).

Giải:

Ta có: \(MN+PN=15cm\) và \(MN-PN=5cm\)

\(\Rightarrow\) \(\left\{{}\begin{matrix}MN=\dfrac{15+5}{2}=10\left(cm\right)\\PN=\dfrac{15-5}{2}=5\left(cm\right)\end{matrix}\right.\)

\(\Rightarrow MN>PN\)

Theo định lí 1 ta suy ra \(\widehat{P}>\widehat{M}\)

Ví dụ 5: Cho tam giác \(ABC\) cân tại \(B\) có chu vi là \(25cm\) và \(AB=7cm\). So sánh các góc của tam giác \(ABC\).

Giải:

Do tam giác \(ABC\) cân tại \(B\) nên \(AB=BC=7cm\)

Mà chu vi tam giác \(ABC\) là \(25cm\) nên \(AB+BC+AC=25\left(cm\right)\)

\(\Rightarrow AC=25-7-7=11\left(cm\right)\)

Ta nhận thấy tam giác \(ABC\) có \(AB=BC< AC\)

Theo định lí 1 ta suy ra \(\widehat{C}=\widehat{A}< \widehat{B}\)

2. Cạnh đối diện với góc lớn hơn

Định lí 2:

Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

Cụ thể, trong tam giác \(ABC\) nếu \(\widehat{B}>\widehat{C}\) thì \(AC>AB\)

Nhận xét:

      +) Định lí 2 là định lí đảo của định lí 1. Từ đó: trong tam giác \(ABC\), \(AC>AB\Leftrightarrow\widehat{B}>\widehat{C}\).

      +) Trong một tam giác tù (hoặc tam giác vuông), góc tù (hoặc góc vuông) là góc lớn nhất nên cạnh đối diện với góc tù (hoặc góc vuông) là cạnh lớn nhất.

Ví dụ: +) Tam giác \(ABC\) có \(\widehat{A}\)  là góc tù thì cạnh \(BC\) là cạnh lớn nhất;

          +) Tam giác \(ABC\) vuông tại \(A\) thì cạnh \(BC\) (cạnh huyền) là cạnh lớn nhất.

Ví dụ 1: Cho tam giác \(ABC\) có \(\widehat{A}=35^0;\widehat{C}=70^0\). So sánh các cạnh của tam giác \(ABC\).

Giải:

Xét trong tam giác \(ABC\) có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) (tổng 3 góc trong tam giác)

\(\Rightarrow\widehat{B}=180^0-\widehat{A}-\widehat{C}=180^0-35^0-70^0=75^0\)

Do \(35^0< 70^0< 75^0\) \(\Rightarrow\widehat{A}< \widehat{C}< \widehat{B}\)

Theo định lí 2 ta suy ra \(BC< AB< AC\).

Ví dụ 2: Cho tam giác \(MNP\) có \(\widehat{M}:\widehat{N}:\widehat{P}=4:3:2\). So sánh các cạnh của tam giác \(MNP\).

Giải:

Ta có \(\widehat{M}:\widehat{N}:\widehat{P}=4:3:2\) \(\Rightarrow\) \(\dfrac{\widehat{M}}{4}=\dfrac{\widehat{N}}{3}=\dfrac{\widehat{P}}{2}\)

\(\Rightarrow\widehat{M}>\widehat{N}>\widehat{P}\)

Theo định lí 2 ta suy ra \(NP>PM>MN\).

Ví dụ 3: Cho tam giác \(ABC\) có \(AB>AC\). Kẻ tia phân giác \(BN,CM\) của góc \(\widehat{B}\) và góc \(\widehat{C}\). Biết \(BN,CM\) cắt nhau tại \(I\). So sánh \(IB\) và \(IC\).

Giải:

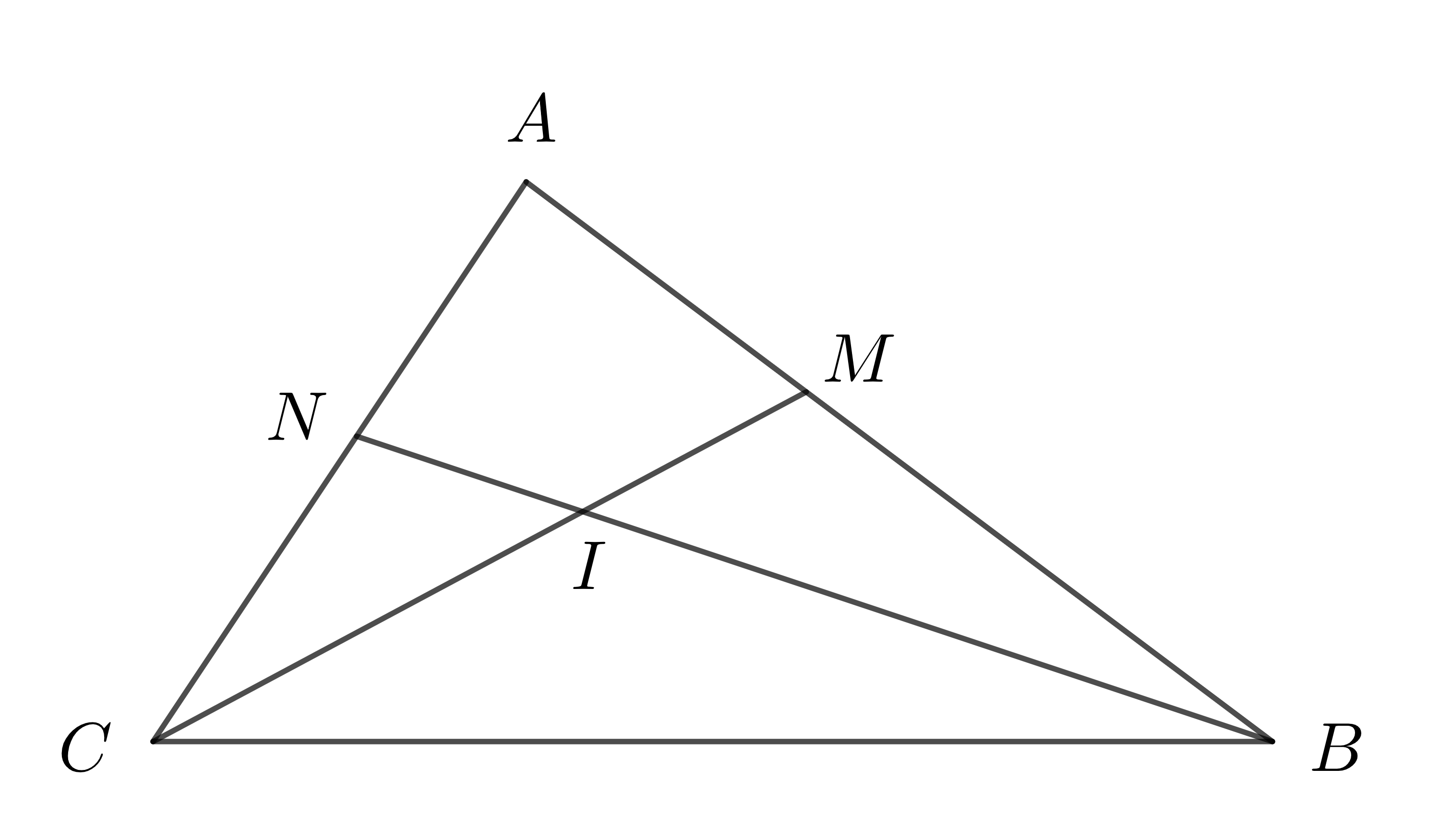
Do \(AB>AC\) nên theo định lí 1 ta có \(\widehat{ACB}>\widehat{ABC}\) 

Vì \(BN\) là tia phân giác góc \(\widehat{ABC}\) nên \(\widehat{NBC}=\dfrac{\widehat{ABC}}{2}\) (tính chất phân giác)

Tương tự ta cũng có \(\widehat{MCB}=\dfrac{\widehat{ACB}}{2}\)

Do \(\widehat{ACB}>\widehat{ABC}\) nên \(\dfrac{\widehat{ACB}}{2}>\dfrac{\widehat{ABC}}{2}\) 

\(\Rightarrow\) \(\widehat{MCB}>\widehat{NBC}\) hay \(\widehat{ICB}>\widehat{IBC}\)

Ta nhận thấy \(\Delta ICB\) có \(\widehat{ICB}>\widehat{IBC}\)

Theo định lí 2 ta suy ra \(IB>IC\).