Cho tam giác ABC có 3 góc nhọn, kẻ BD vuông AC tại D, CE vuông AB tại E.
1)C/m: BC>BD
2)C/m: BC>CE
3)C/m: BC> (BD+CE):2
Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
1: Vì ΔBDC vuông tại D
nên BC>BD
2: Vì ΔBCE vuông tại E
nên BC>CE
3: BC>BD
BC>CE
Do đó: 2BC>BD+CE
hay \(BC>\dfrac{BD+CE}{2}\)
Đúng 0
Bình luận (0)
Cho điểm M nằm trong tam giác ABC.
Vẽ các điểm E, D, F lần lượt là hình chiếu của M lên AB, CB, AC. Chứng minh : MF + MD + MF < MA +MB + MC.Bài 1: Cho tam giác ABC có góc C góc B. Kẻ AH ⊥ BC tại H. So sánh HB và HC
Bài 2: Cho tam giác nhọn MNK, MN MK. Từ M kẻ MH ⊥ NK (H thuộc NK). Trên tia HK lấy điểm E sao cho NHHE. Từ N kẻ NA ⊥ MK (A thuộc MK). Trên tia MA lấy điểm P sao cho MNNP. Chứng minh rằng:
a) MNME
b) MAAP
Bài 3: Cho tam giác ABC, có AB AC. Từ A hạ AH ⊥ BC. Trên đoạn thẳng AH lấy điểm M (M không trùng A, H). Chứng minh rằng:
a) MB MC
b) BA BM
Bài 4: Cho đường thẳng a và điểm A nằm ngoài đường thẳng a. Gọi H là h...
Đọc tiếp
Bài 1: Cho tam giác ABC có góc C > góc B. Kẻ AH ⊥ BC tại H. So sánh HB và HC
Bài 2: Cho tam giác nhọn MNK, MN < MK. Từ M kẻ MH ⊥ NK (H thuộc NK). Trên tia HK lấy điểm E sao cho NH=HE. Từ N kẻ NA ⊥ MK (A thuộc MK). Trên tia MA lấy điểm P sao cho MN=NP. Chứng minh rằng:
a) MN=ME
b) MA=AP
Bài 3: Cho tam giác ABC, có AB > AC. Từ A hạ AH ⊥ BC. Trên đoạn thẳng AH lấy điểm M (M không trùng A, H). Chứng minh rằng:
a) MB > MC
b) BA > BM
Bài 4: Cho đường thẳng a và điểm A nằm ngoài đường thẳng a. Gọi H là hình chiếu của điểm A xuống đường thẳng a. Trên đường thẳng a lấy hai điểm B và C. Tính độ dài các đường xiên AB, AC biết AH=6cm, HB=8cm và HC=10cm.
Bài 5: Cho tam giác ABC vuông tại A. Gọi H là hình chiếu của A trên BC. Biết góc BAH < góc CAH. Chứng minh rằng: HB < HC.
Bài 1:
\(\widehat{C}>\widehat{B}\) nên AB>AC
Xét ΔABC có AB>AC
mà HB là hình chiếu của AB trên BC
và HC là hình chiếu của AC trên BC
nên HB>HC
Đúng 0
Bình luận (0)
Cho \(\widehat{xOy}=90^o.\) Vẽ cung tròn tâm O, bán kính tùy ý, cắt Ox tại A, cắt Oy tại B. Từ một điểm C tùy ý trên cung AB ( C khác A, B), kẻ đường thẳng song song với BC, cắt Ox tại A', cắt Oy tại B'. CMR \(CA'^2+CB'^2\) không phụ thuộc vào vị trí điểm C trên cung AB.
Cho tam giác ABC nhọn. Các đường phân giác của góc B và góc C cắt nhau tại O.Chứng minh rằng AO là phân giác của góc BAC
cái này là định lí luôn rồi đâu cần chứng minh
Đúng 0
Bình luận (1)
cho tam giác ABC , tia phân giác của góc B và góc C cắt nhau tại I.Kẻ IH vuông góc AB và IK vuông góc AC ( H thuộc AB , K thuộc AC ) Chứng minh rằng IH = IK
Xét ΔAHI vuông tại H và ΔAKI vuông tại K có
AI chung
\(\widehat{HAI}=\widehat{KAI}\)
Do đó: ΔAHI=ΔAKI
Suy ra: IH=IK
Đúng 0
Bình luận (0)
Cho tam giác abc Vuông tại a. Trên Ab lấy điểm d. Trên ac lấy điểm E. a. CM DC< BCb. CM DE<BC
Giúp mình nha
a: Ta có: ΔADC vuông tại A
nên \(\widehat{ADC}< 90^0\)
=>\(\widehat{CDB}>90^0\)
=>DC<BC(1)
b: Ta có:ΔAED vuông tại A
nên \(\widehat{AED}< 90^0\)
=>\(\widehat{CED}>90^0\)
=>DE<CD(2)
Từ (1)và (2) suy ra DE<BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A( AB<AC), phân giác BD. Đường thẳng qua C Vuông góc với AC cắt BD tại M.a) Chứng minh tam giác CBM cân.b) so sánh CM va CA. c) So sánh AM và BC Giúp mình với, cần gấp
a: Xét ΔCBM có \(\widehat{CBM}=\widehat{CMB}\)
nen ΔCBM cân tại C
b: Ta có: CM=CB
mà CB>CA
nên CM>CA
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a, tia phân giác của góc b cắt ac tại d, cắt đường thẳng vẽ từ c vuông gó với actaij e
so sánh bd và ce
Chứng minh rằng trong một tam giác cân, độ dài đoạn thẳng nối đỉnh đối diện với đáy và một điểm bất kỳ của cạnh đáy nhỏ hơn hoặc bằng độ dài của cạnh bên.
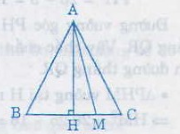
Xét tam giác ABC cân tại A Gọi D là điểm bất kì của cạnh đáy BC Kẻ đường cao AH ta có :
- Nếu \(D\equiv B\) hoặc C thì AD = AB = AC
- Nếu \(D\equiv H\) thì AD < AB ( hoặc AD < AC )
- Nếu D không trùng B ; C ; H giả sử D nằm giữa D và H thì trong tam giác ABH có BH và DH lần lượt là hình chiếu của AB và AD
Ta có : HD < HB nên suy ra AD < AB
Từ 3 điều trên trong 1 tam giác cân độ dài đoạn thẳng nối đỉnh đối diện với đáy và một điểm bất kỳ của cạnh đáy nhỏ hơn hoặc bằng độ dài của cạnh bên ( đpcm )
Đúng 0
Bình luận (2)













