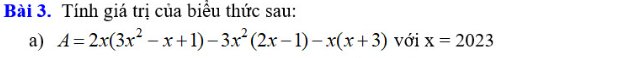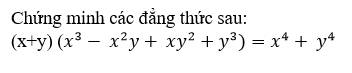Bài 2: Nhân đa thức với đa thức
Cậu cần bài nào nhỉ ? Cần hết thì tách ra từng bài thôi nha cậuu
Đúng 0
Bình luận (1)
1:
a: =x^3-6x^2+12x-8
b: (2x-3y)^3
=8x^3-36x^2y+54xy^2-27y^3
c: (x+y/x)^3
=x^3+3xy+3y^2/x+y^3/x^3
2:
a: =(x-3)^3
b: =(-1/2x+1)^3
c: =(x^2-1/2y)^3
Đúng 1
Bình luận (0)
Với a,b,c thuộc R thỏa mãn : (3a+3b+3c)324+(3a+b−c)3+(3b+c−a)3+(3c+a−b)3(3a+3b+3c)324+(3a+b−c)3+(3b+c−a)3+(3c+a−b)3CMR : (a+2b)(b+2c)(c+2a)1
Đọc tiếp
Với a,b,c thuộc R thỏa mãn :
CMR : (a+2b)(b+2c)(c+2a)=1
Lời giải:
Đặt ⎧⎪⎨⎪⎩3a+b−c=x3b+c−a=y3c+a−b=z{3a+b−c=x3b+c−a=y3c+a−b=z
Khi đó, điều kiện đb tương đương với:
(x+y+z)3=24+x3+y3+z3⇔3(x+y)(y+z)(x+z)=24(x+y+z)3=24+x3+y3+z3⇔3(x+y)(y+z)(x+z)=24
⇔3(2a+4b)(2b+4c)(2c+4a)=24⇔3(2a+4b)(2b+4c)(2c+4a)=24
⇔(a+2b)(b+2c)(c+2a)=1⇔(a+2b)(b+2c)(c+2a)=1
Do đó ta có đpcm
Đúng 1
Bình luận (0)
Lời giải:
Đặt ⎧⎪⎨⎪⎩3a+b−c=x3b+c−a=y3c+a−b=z{3a+b−c=x3b+c−a=y3c+a−b=z
Khi đó, điều kiện đb tương đương với:
(x+y+z)3=24+x3+y3+z3⇔3(x+y)(y+z)(x+z)=24(x+y+z)3=24+x3+y3+z3⇔3(x+y)(y+z)(x+z)=24
⇔3(2a+4b)(2b+4c)(2c+4a)=24⇔3(2a+4b)(2b+4c)(2c+4a)=24
⇔(a+2b)(b+2c)(c+2a)=1⇔(a+2b)(b+2c)(c+2a)=1
Do đó ta có đpcm
Đúng 1
Bình luận (0)
x mũ3 - 3x bình y + x+3xy bình -y-y mũ3
`x^3 - 3x^2y + x + 3xy^2 - y - y^3`
`=(x)^3 - 3*(x)^2*y + 3*x*y^2 - (y)^3 + (x - y)`
`= (x - y)^3 + (x - y)`
`= (x - y)[(x - y)^2 + 1]`
`= (x - y)(x - y - 1)(x - y + 1)`
____
`@` CT:
`(A - B)^3=A^3-3A^2B+3AB^2- B^3`
Đúng 2
Bình luận (0)
2X x(3X^2-5X+3) mọi người giải giúp em với ạ
\(2x\left(3x^2-5x+3\right)\\ \)
\(=6x^3-10x^2+6x\)
Đúng 2
Bình luận (0)
A=6x^3-2x^2+2x-6x^3+3x^2-x^2-3x
=-x
=-2023
Đúng 0
Bình luận (0)
`A=2x(3x^2-x+1)-3x^2(2x-1)-x(x+3)`
`= 6x^3 -2x^2 +2x-(6x^3 -3x^2)-(x^2+3x)`
`=6x^3 -2x^2 +2x-6x^3 +3x^2 -x^2-3x`
`=(6x^3 -6x^3 )+(-2x^2 +3x^2-x^2)+(2x-3x)`
`= -x`
Thay `x=2023` vào `-x`
Ta có : `-x=-2023`
Đúng 1
Bình luận (0)
Hơn một năm rùi mới vào lại đây kỉ niệm ghê:))
\(VT=(x+y)(x^3-x^2y+xy^2+y^3)\\=x(x^3-x^2y+xy^2+y^3)+y(x^3-x^2y+xy^2+y^3)\\=x^4-x^3y+x^2y^2+xy^3+x^3y-x^2y^2+xy^3+y^4\\=x^4+y^4+(-x^3y+x^3y)+(x^2y^2-x^2y^2)+(xy^3+xy^3)\\=x^4+y^4+2xy^3\)
Cậu xem lại đề giúp mình nhé!
Đúng 1
Bình luận (0)
\(VT=\left(x+y\right)\left(x^3-x^2y+xy^2+y^3\right)\)
`= x^4 -x^3y+x^2y^2+xy^3 +x^3y-x^2y^2 +xy^3 +y^4`
`= (-x^3y +x^3y) +(x^2y^2-x^2y^2) +(xy^3 +xy^3) +x^4+y^4`
`= 2xy^3+x^4+y^4`
Đề có sai ko c...
Đúng 1
Bình luận (0)
a. ( 5 - 2x ) ( 5x + 2x ) + 2x ( x + 3 ) = 4 - 2x² b. ( 3x - 2 )( -2x) + 5x² = -x( x - 3) c. 7 - ( 3 + 2x ) (2x - 3 ) = ( x + 4 )²
a: Sửa đề: (5-2x)(5+2x)+2x(x+3)=4-2x^2
=>25-4x^2+2x^2+6x=4-2x^2
=>6x+25=4
=>6x=-21
=>x=-7/2
b: (3x-2)(-2x)+5x^2=-x(x-3)
=>-6x^2+4x+5x^2=-x^2+3x
=>4x=3x
=>x=0
c: =>7-(4x^2-9)=x^2+8x+16
=>7-4x^2+9-x^2-8x-16=0
=>-5x^2-8x=0
=>5x^2+8x=0
=>x(5x+8)=0
=>x=0 hoặc x=-8/5
Đúng 0
Bình luận (0)
Làm ơn giúp với ạ!Hình ảnh trên mô tả cách để làm hình hộp chữ nhật có 3 kích thước là x,y,z(cm) . Các kích thước và tỉ lệ của hộp phụ thuộc vào các giá trị của x,y,z .tính diện tích các mặt của hình hộp chữ nhật được thể hiện qua hình đó.
Đọc tiếp
Làm ơn giúp với ạ!
Hình ảnh trên mô tả cách để làm hình hộp chữ nhật có 3 kích thước là x,y,z(cm) . Các kích thước và tỉ lệ của hộp phụ thuộc vào các giá trị của x,y,z .tính diện tích các mặt của hình hộp chữ nhật được thể hiện qua hình đó.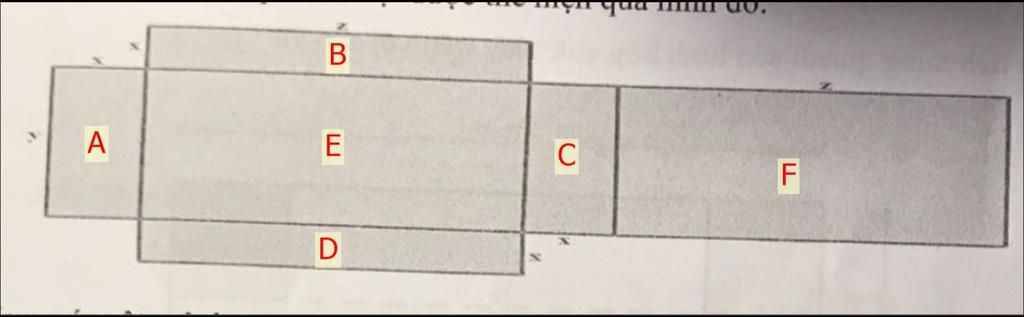
Bài 4 tìm x A, 3x+2(5-x)=0 B, x(2x-1)(x+5)-(2x^2+1)(x+4,5)=3,5 C, 3x^2-3x(x-2)=36 D, (3x^2-x+1)(x-1)+x^2(4-3x)=5/2
a: =>3x+10-2x=0
=>x+10=0
=>x=-10
b: =>x(2x^2+9x-5)-(2x^3+9x^2+x+4,5)=3,5
=>2x^3+9x^2-5x-2x^3-9x^2-x-4,5=3,5
=>-6x=8
=>x=-4/3
c: =>3x^2-3x^2+6x=36
=>6x=36
=>x=6
Đúng 0
Bình luận (0)